题目内容
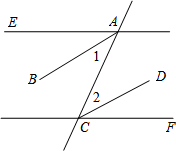 如图,直线AE、CF分别被直线AC所截,已知AE∥FC,AB平分∠EAC,CD平分∠ACF,将下列说明AB∥CD的过程及理由填写完整.
如图,直线AE、CF分别被直线AC所截,已知AE∥FC,AB平分∠EAC,CD平分∠ACF,将下列说明AB∥CD的过程及理由填写完整.理由:∵AE∥FC(已知)
∴∠EAC=∠
∵AB平分∠EAC,CD平分∠ACF(已知)
∴∠
| 1 |
| 2 |
| 1 |
| 2 |
∴∠
∴AB∥CD(
考点:平行线的判定与性质
专题:推理填空题
分析:根据“两直线平行,内错角相等”推知:∠EAC=∠ACF;然后结合已知条件,利用等量代换判定内错角∠1=∠2,则由“内错角相等,两直线平行”证得结论.
解答:解:∵AE∥FC(已知),
∴∠EAC=∠ACF,(两直线平行,内错角相等),
∵AB平分∠EAC,CD平分∠ACF(已知),
∴∠1=
∠EAC,∠2=
∠ACF(角平分线的定义),
∴∠1=∠2(等量代换),
∴AB∥CD( 内错角相等,两直线平行).
故答案是:ACF;两直线平行,内错角相等;1;ACF;1;内错角相等,两直线平行.
∴∠EAC=∠ACF,(两直线平行,内错角相等),
∵AB平分∠EAC,CD平分∠ACF(已知),
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1=∠2(等量代换),
∴AB∥CD( 内错角相等,两直线平行).
故答案是:ACF;两直线平行,内错角相等;1;ACF;1;内错角相等,两直线平行.
点评:本题考查了平行线的判定与性质.解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
下列命题是假命题的是( )
| A、平行四边形的对边相等 |
| B、四条边都相等的四边形是菱形 |
| C、矩形的两条对角线互相垂直 |
| D、对角线互相平分的四边形是平行四边形 |
下列各点中,在反比例函数y=-
的图象上是( )
| 7 |
| x |
| A、(-1,7) |
| B、(2,3.5) |
| C、(1,7) |
| D、(-2,-3.5) |
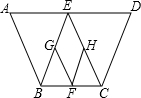 如图,等腰梯形ABCD中,AD∥BC,AB=CD,点E是线段AD上的一个动点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.
如图,等腰梯形ABCD中,AD∥BC,AB=CD,点E是线段AD上的一个动点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.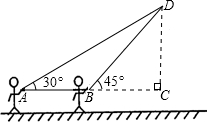 放风筝是大家喜爱的一种运动.星期天的上午小明在大洲广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树的树梢上,风筝固定在了D处.此时风筝线AD与水平线的夹角为30°,AD=8米,为了便于观察.小明迅速向前边移动边收线到达了B处,此时风筝线BD与水平线的夹角为45°.已知点A、B、C在冋一条直线上,∠ACD=90°.请你求出小明此吋所收回的风筝线的长度是多少米?
放风筝是大家喜爱的一种运动.星期天的上午小明在大洲广场上放风筝.如图他在A处时不小心让风筝挂在了一棵树的树梢上,风筝固定在了D处.此时风筝线AD与水平线的夹角为30°,AD=8米,为了便于观察.小明迅速向前边移动边收线到达了B处,此时风筝线BD与水平线的夹角为45°.已知点A、B、C在冋一条直线上,∠ACD=90°.请你求出小明此吋所收回的风筝线的长度是多少米? 如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,则sinA=
如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,则sinA= 用小立方块搭一个几何体,使从正面和上面看到的图形如图所示,并画出.
用小立方块搭一个几何体,使从正面和上面看到的图形如图所示,并画出.