题目内容
如图，已知AC∥FE，AD=FB，点A、D、B、F在一条直线上，要使△ABC≌△FDE，还需添加一个条件，这个条件可以是考点：全等三角形的判定
专题：开放型
分析：要判定△ABC≌△FDE，已知AC∥FE，AD=BF，则AB=CF，具备了一组角和一组边对应相等，故可以添加AC=FE，利用SAS可证全等．（也可添加其它条件）．
解答：解：增加一个条件：AC=FE，
∵AC∥FE，
∴∠A=∠F．
显然能看出，在△ABC和△FDE中，利用SAS可证三角形全等（答案不唯一）．
故答案为：AC=FE（答案不唯一）．
∵AC∥FE，
∴∠A=∠F．
显然能看出，在△ABC和△FDE中，利用SAS可证三角形全等（答案不唯一）．
故答案为：AC=FE（答案不唯一）．
点评：本题考查了全等三角形的判定；判定方法有ASA、AAS、SAS、SSS等，在选择时要结合其它已知在图形上的位置进行选取．
练习册系列答案
相关题目
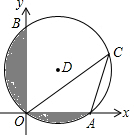如图，在平面直角坐标系中，已知⊙D经过原点O，与x轴、y轴分别交于A、B两点，点B坐标为（0，2
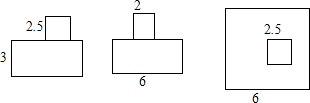已知一个模型的三视图如图所示，（单位：m）
如图，AB是⊙O的直径，E是⊙O上的一点，C是弧AE的中点，若∠A=50°，则∠AOE的度数为
从三个不同方向看一个几何体，得到的平面图形如图所示，则这个几何体是（ ）| A、圆柱 | B、圆锥 | C、棱锥 | D、球 |