题目内容
如图，O是△ABC内一点，∠ACB=60°，∠α=∠β，则∠O=考点：三角形内角和定理
专题：
分析：由∠ACB=60°，∠α=∠β，可得：∠α+∠OCB=60°，然后根据三角形内角和定理，可求∠O的度数．
解答：解：∵∠ACB=60°，
∴∠β+∠OCB=∠ACB=60°，
∵∠α=∠β，
∴∠α+∠OCB=60°，
∵∠O+∠α+∠OCB=180°，
∴∠O=180°-60°=120°．
故答案为：120°．
∴∠β+∠OCB=∠ACB=60°，
∵∠α=∠β，
∴∠α+∠OCB=60°，
∵∠O+∠α+∠OCB=180°，
∴∠O=180°-60°=120°．
故答案为：120°．
点评：此题考查了三角形内角和定理，解题的关键是：由∠ACB=60°，∠α=∠β，得到：∠α+∠OCB=60°．
练习册系列答案
相关题目
已知∠α，∠β，利用尺规作∠AOB=∠α-∠β．
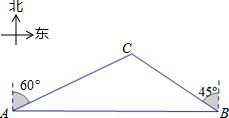如图，一天，我国一渔政船航行到A处时，发现正东方向的我领海区域B处有一可疑渔船，可疑渔船正向西北方向航行，我渔政船立即沿北偏东60°方向航行，在我领海区域的C处截获可疑渔船．我渔政船的航行路程AC为18是海里，问可疑渔船的航行路程BC是多少海里？（结果保留根号）
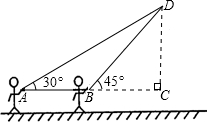放风筝是大家喜爱的一种运动．星期天的上午小明在大洲广场上放风筝．如图他在A处时不小心让风筝挂在了一棵树的树梢上，风筝固定在了D处．此时风筝线AD与水平线的夹角为30°，AD=8米，为了便于观察．小明迅速向前边移动边收线到达了B处，此时风筝线BD与水平线的夹角为45°．已知点A、B、C在冋一条直线上，∠ACD=90°．请你求出小明此吋所收回的风筝线的长度是多少米？
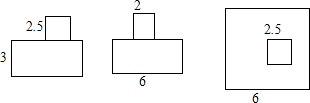已知一个模型的三视图如图所示，（单位：m）
如图，在Rt△ABC中，∠C=90°，AB=10，BC=6，则sinA=