题目内容
10.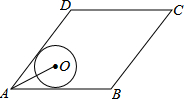 如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )| A. | 5 | B. | 6 | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
分析 如图作DH⊥AB于H,连接BD,延长AO交BD于E.利用菱形的面积公式求出DH,再利用勾股定理求出AH,BD,由△AOF∽△DBH,可得$\frac{OA}{BD}$=$\frac{OF}{BH}$,即可解决问题.
解答 解:如图作DH⊥AB于H,连接BD,延长AO交BD于E.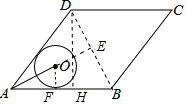
∵菱形ABCD的边AB=20,面积为320,
∴AB•DH=32O,
∴DH=16,
在Rt△ADH中,AH=$\sqrt{A{D}^{2}-D{H}^{2}}$=12,
∴HB=AB-AH=8,
在Rt△BDH中,BD=$\sqrt{D{H}^{2}+B{H}^{2}}$=8$\sqrt{5}$,
设⊙O与AB相切于F,连接OF.
∵AD=AB,OA平分∠DAB,
∴AE⊥BD,
∵∠OAF+∠ABE=90°,∠ABE+∠BDH=90°,
∴∠OAF=∠BDH,∵∠AFO=∠DHB=90°,
∴△AOF∽△DBH,
∴$\frac{OA}{BD}$=$\frac{OF}{BH}$,
∴$\frac{10}{8\sqrt{5}}$=$\frac{OF}{8}$,
∴OF=2$\sqrt{5}$.
故选C.
点评 本题考查切线的性质、菱形的性质、勾股定理、相似三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.如图1,在矩形ABCD中,动点E从A出发,沿AB→BC方向运动,当点E到达点C时停止运动,过点E做FE⊥AE,交CD于F点,设点E运动路程为x,FC=y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是$\frac{2}{5}$,则矩形ABCD的面积是( )
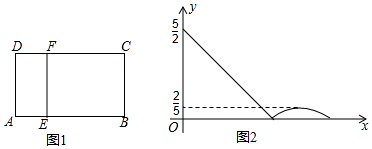

| A. | $\frac{23}{5}$ | B. | 5 | C. | 6 | D. | $\frac{25}{4}$ |
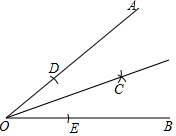 如图所示,已知∠AOB=40°,现按照以下步骤作图:
如图所示,已知∠AOB=40°,现按照以下步骤作图: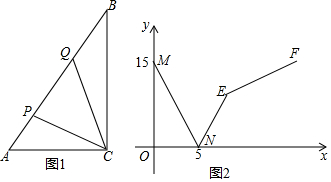
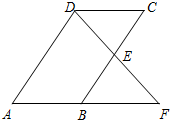 已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.
已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.