题目内容
5.如图1,在△ABC中,∠C=90°,AC=9cm,动点P从点A以1cm/s的速度沿AB向点B运动,运动到点B终止,同时动点Q从点B沿BA向点A匀速运动,运动到点A终止.设运动时间为x(s),P、Q之间的距离为y(cm),且y与x的函数图象如图2所示.(1)动点Q的运动速度为2s.
(2)点N所表示的实际意义是点P、Q运动5s时相遇.
(3)若△PQC的面积为18cm2,求运动的时间x.
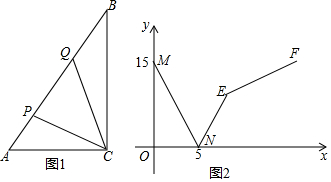
分析 (1)根据图2知道,AB=15,结合P、Q相遇的时间是5s来求点Q的运动速度;
(2)点N处的纵坐标为0,即点P、Q相遇;
(3)作CD⊥AB,由等积法求得CD的长度,结合三角形的面积公式解答即可.
解答  解:(1)根据图2知道,AB=15,且点P、Q相遇的时间是5s.
解:(1)根据图2知道,AB=15,且点P、Q相遇的时间是5s.
由题意得:$\frac{15}{5}$-1=2(s).
故答案是:2cm/s;
(2)由图2知,点N处的纵坐标为0,即点P、Q相遇,所以点N表示点P、Q运动5s时相遇.
故答案是:点P、Q运动5s时相遇;
(3)作CD⊥AB,
由函数图象可知AB=15cm,
又∠C=90°,AC=9cm,
∴BC=12cm
∵$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD
∴CD=7.2cm.
∵S△PQC=18,
∴$\frac{1}{2}$PQ•CD=18,
∴PQ=5.
yMN=-3x+15,
又∵-3x+15=5(0≤x≤5),
∴x=$\frac{10}{3}$,
又∵yNE=3x-15(5≤x<7.5)
∴x=$\frac{20}{3}$.
∴当运动时间为$\frac{10}{3}$s或$\frac{20}{3}$s.时S△PQC=18.
点评 本题考查了三角形综合题,需要掌握待定系数法求一次函数解析式,三角形的面积公式,勾股定理以及动点问题.对应动点问题,要分类讨论,以防漏解或错解.还需要学生具备一定的读图能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.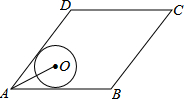 如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
 如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )| A. | 5 | B. | 6 | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
17.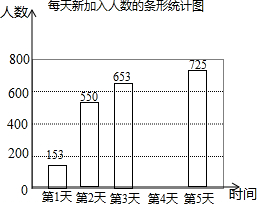 某数学学习网站为吸引更多人注册加入,举行了一个为期5天的推广活动,在活动期间,加入该网站的人数变化情况如下表所示:
某数学学习网站为吸引更多人注册加入,举行了一个为期5天的推广活动,在活动期间,加入该网站的人数变化情况如下表所示:
(1)表格中a=4556,b=600;
(2)请把下面的条形统计图补充完整;
(3)根据以上信息,下列说法正确的是①(只要填写正确说法前的序号).
①在活动之前,该网站已有3200人加入;
②在活动期间,每天新加入人数逐天递增;
③在活动期间,该网站新加入的总人数为2528人.
 某数学学习网站为吸引更多人注册加入,举行了一个为期5天的推广活动,在活动期间,加入该网站的人数变化情况如下表所示:
某数学学习网站为吸引更多人注册加入,举行了一个为期5天的推广活动,在活动期间,加入该网站的人数变化情况如下表所示:| 时间 | 第1天 | 第2天 | 第3天 | 第4天 | 第5天 |
| 新加入人数(人) | 153 | 550 | 653 | b | 725 |
| 累计总人数(人) | 3353 | 3903 | a | 5156 | 5881 |
(2)请把下面的条形统计图补充完整;
(3)根据以上信息,下列说法正确的是①(只要填写正确说法前的序号).
①在活动之前,该网站已有3200人加入;
②在活动期间,每天新加入人数逐天递增;
③在活动期间,该网站新加入的总人数为2528人.
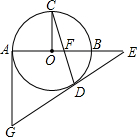 如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE=∠DFE,DE交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.
如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE=∠DFE,DE交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.
 某几何体的三视图如图所示,则此几何体的侧面积为$3\sqrt{73}π$.
某几何体的三视图如图所示,则此几何体的侧面积为$3\sqrt{73}π$. 如图,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,∠1=25°,则∠AED的度数为50°.
如图,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,∠1=25°,则∠AED的度数为50°.