题目内容
15.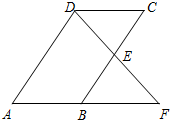 已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.
已知,如图,平行四边形ABCD中,E是BC边的中点,连DE并延长交AB的延长线于点F,求证:AB=BF.
分析 根据线段中点的定义可得CE=BE,根据平行四边形的对边平行且相等可得AB∥CD,AB=CD,再根据两直线平行,内错角相等可得∠DCB=∠FBE,然后利用“角边角”证明△CED和△BEF全等,根据全等三角形对应边相等可得CD=BF,从而得证.
解答 证明:∵E是BC的中点,
∴CE=BE,
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠DCB=∠FBE,
在△CED和△BEF中,$\left\{\begin{array}{l}{∠DCB=∠FBE}&{\;}\\{CE=BE}&{\;}\\{∠CED=∠BEF}&{\;}\end{array}\right.$,
∴△CED≌△BEF(ASA),
∴CD=BF,
∴AB=BF.
点评 本题考查了全等三角形的判定与性质,平行四边形的性质,熟记性质并确定出三角形全等的条件是解题的关键.

练习册系列答案
相关题目
10.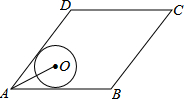 如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
 如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )| A. | 5 | B. | 6 | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
20.已知2x=3y(y≠0),则下面结论成立的是( )
| A. | $\frac{x}{y}$=$\frac{3}{2}$ | B. | $\frac{x}{3}$=$\frac{2}{y}$ | C. | $\frac{x}{y}$=$\frac{2}{3}$ | D. | $\frac{x}{2}$=$\frac{y}{3}$ |
6. 如图,AB∥CD,那么∠1+∠2+∠3+∠4=( )
如图,AB∥CD,那么∠1+∠2+∠3+∠4=( )
 如图,AB∥CD,那么∠1+∠2+∠3+∠4=( )
如图,AB∥CD,那么∠1+∠2+∠3+∠4=( )| A. | 720° | B. | 360° | C. | 180° | D. | 540° |
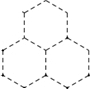 如图,是由大小完全相同的正六边形组成的图形,小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色,则上方的正六边形涂红色的概率是$\frac{1}{3}$.
如图,是由大小完全相同的正六边形组成的图形,小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色,则上方的正六边形涂红色的概率是$\frac{1}{3}$.
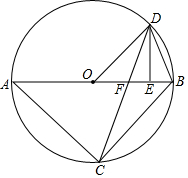 如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.