题目内容
19.先化简,再求值:(1-$\frac{5}{x+2}}$)÷$\frac{{{x^2}-9}}{x+3}$,其中x=$\sqrt{3}$-2.分析 把分式进行化简,再把x的值代入即可求出结果.
解答 解:原式=$\frac{x-3}{x+2}÷\frac{{({x+3})({x-3})}}{x+3}=\frac{x-3}{x+2}•\frac{x+3}{{({x+3})({x-3})}}=\frac{1}{x+2}$.
当$x=\sqrt{3}-2$时,原式=$\frac{1}{{\sqrt{3}-2+2}}=\frac{1}{{\sqrt{3}}}=\frac{{\sqrt{3}}}{3}$.
点评 本题主要考查了分式的混合运算-化简求值问题,在解题时要乘法公式的应用进行化简.

练习册系列答案
相关题目
9.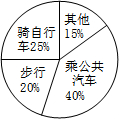 某校学生到校方式情况的统计图如图所示,若该校步行到校的学生有100人,则乘公共汽车到校的学生有( )
某校学生到校方式情况的统计图如图所示,若该校步行到校的学生有100人,则乘公共汽车到校的学生有( )
 某校学生到校方式情况的统计图如图所示,若该校步行到校的学生有100人,则乘公共汽车到校的学生有( )
某校学生到校方式情况的统计图如图所示,若该校步行到校的学生有100人,则乘公共汽车到校的学生有( )| A. | 75人 | B. | 100人 | C. | 125人 | D. | 200人 |
10.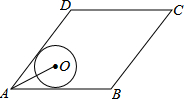 如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
 如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )| A. | 5 | B. | 6 | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{2}$ |
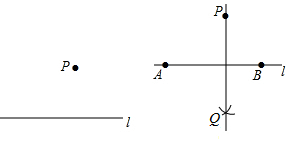
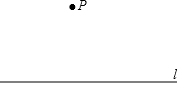
 如图,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,∠1=25°,则∠AED的度数为50°.
如图,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,∠1=25°,则∠AED的度数为50°.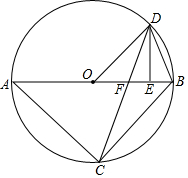 如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F. 按如图所示的程序计算,若开始输入x的值为6,我们发现第一次得到的结果为3,第2次得到的结果为10,第3次得到的结果为5…请你探索第2017次得到的结果为10.
按如图所示的程序计算,若开始输入x的值为6,我们发现第一次得到的结果为3,第2次得到的结果为10,第3次得到的结果为5…请你探索第2017次得到的结果为10.