题目内容
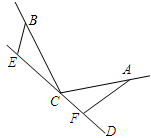如图，直线CD经过∠BCA的顶点C，CA=CB，E，F分别是直线上CD上的两点，且∠BEC=∠CFA=∠α，如图，若直线CD经过∠BCA的外部，∠α=∠BCA，请探究EF与BE，AF三条线段的数量关系，并证明．考点：全等三角形的判定与性质
专题：
分析：只要通过条件证明△BEC≌△CFA（可通过ASA证得），可得BE=CF，EC=AF，即可得到EF=EC+CF=BE+AF．
解答：探究结论：EF=BE+AF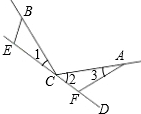
，
证明：∵∠1+∠2+∠BCA=180°，∠2+∠3+∠CFA=180°
又∵∠BCA=∠α=∠CFA，
∴∠1=∠3；
在△BEC和△CFA中，
，
∴△BEC≌△CFA（AAS），
∴BE=CF，EC=FA，
∴EF=EC+CF=BE+AF．
，证明：∵∠1+∠2+∠BCA=180°，∠2+∠3+∠CFA=180°
又∵∠BCA=∠α=∠CFA，
∴∠1=∠3；
在△BEC和△CFA中，
|
∴△BEC≌△CFA（AAS），
∴BE=CF，EC=FA，
∴EF=EC+CF=BE+AF．
点评：本题主要考查全等三角形全等的判定，涉及到三角形内角和定理，线段比较长短等知识点．属于一道较复杂的基础题．
练习册系列答案
高中必刷题系列答案
相关题目
如图，在Rt△ABC中，∠C=90°，∠A=30°，斜边AB=2，求：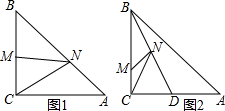
在△ABC中，∠ACB=90°，AC=BC=2，M是BC边上一点．
在下列四个条件中：①AB=DC；②BE=CE；③∠B=∠C；④∠BAE=∠CDE．请选出两个作为条件，得出AE=DE（写出一种即可），并加以证明．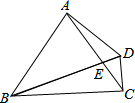
如图，△ABC是等边三角形，BD=AB，BD与AC交于点E，当点E在AC上运动时，∠ADC的大小是否发生变化？如果变化，请说明变化的范围，如果不变，请说明理由．