题目内容
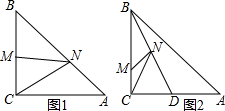 在△ABC中,∠ACB=90°,AC=BC=2,M是BC边上一点.
在△ABC中,∠ACB=90°,AC=BC=2,M是BC边上一点.(1)如图1,若M是BC中点,N为AB上任意一点,求MN+CN的最小值;
(2)如图2,BD平分∠ABC,点M、N分别是BC、BD上任意一点,求MC+CN的最小值.
考点:轴对称-最短路线问题
专题:
分析:(1)根据平面内线段最短,构建直角三角形,解直角三角形即可.
(2)根据已知条件结合图形构造全等三角形,利用三角形的三边的关系确定线段和的最小值.
(2)根据已知条件结合图形构造全等三角形,利用三角形的三边的关系确定线段和的最小值.
解答: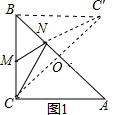 解:(1)如图1,过点作CO⊥AB于O,延长BO到B',使OC'=OC,连接MC',交AB于N,
解:(1)如图1,过点作CO⊥AB于O,延长BO到B',使OC'=OC,连接MC',交AB于N,
此时MC'=MN+NC'=MN+CN的值最小,
连接BC',
∵CO⊥AB,AC=BC,∠ABC=90°,
∴∠BCO=
×90°=45°,
∵CO=OC',CO⊥AB,
∴BC'=CB=2,
∴∠OC'B=∠OCB=45°,
∴∠C'BC=90°,
∴C'B⊥BC,
∴MC′=
=
=
,
∴MB'的长度就是BN+MN的最小值为
.
(2)如图2,在BA上截取BM=BM′,连接CM′.
∵在△ABC中,∠ACB=90°,AC=BC=2,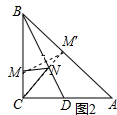
∴AB=
=2
,
∵BD平分∠ABC,
∴∠NBM=∠NBM′,
在△BMN与△BM′N中,
,
∴△BMN≌△BM′N(SAS),
∴MN=M′N.
∴MN+CN=CN+M′N≥CM′.
∵CN+MN有最小值.
当CM′是点C到直线AB的距离时,CM′为最小值,
所以CN+MN的最小值是
AB=
×2
=
.
故CN+MN的最小值是
.
 解:(1)如图1,过点作CO⊥AB于O,延长BO到B',使OC'=OC,连接MC',交AB于N,
解:(1)如图1,过点作CO⊥AB于O,延长BO到B',使OC'=OC,连接MC',交AB于N,此时MC'=MN+NC'=MN+CN的值最小,
连接BC',
∵CO⊥AB,AC=BC,∠ABC=90°,
∴∠BCO=
| 1 |
| 2 |
∵CO=OC',CO⊥AB,
∴BC'=CB=2,
∴∠OC'B=∠OCB=45°,
∴∠C'BC=90°,
∴C'B⊥BC,
∴MC′=
| BC′2+BM2 |
| 22+12 |
| 5 |
∴MB'的长度就是BN+MN的最小值为
| 5 |
(2)如图2,在BA上截取BM=BM′,连接CM′.
∵在△ABC中,∠ACB=90°,AC=BC=2,

∴AB=
| AC2+BC2 |
| 2 |
∵BD平分∠ABC,
∴∠NBM=∠NBM′,
在△BMN与△BM′N中,
|
∴△BMN≌△BM′N(SAS),
∴MN=M′N.
∴MN+CN=CN+M′N≥CM′.
∵CN+MN有最小值.
当CM′是点C到直线AB的距离时,CM′为最小值,
所以CN+MN的最小值是
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故CN+MN的最小值是
| 2 |
点评:此题考查了线路最短的问题,确定动点N为何位置时,使MN+CN的值最小是关键.

练习册系列答案
相关题目
化简
的结果为( )
| ||
| a |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
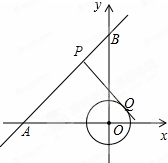 如图,在平面直角坐标系xOy中,直线AB经过点A(-6,0)、B(0,6),⊙O的半径为3(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为
如图,在平面直角坐标系xOy中,直线AB经过点A(-6,0)、B(0,6),⊙O的半径为3(O为坐标原点),点P在直线AB上,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为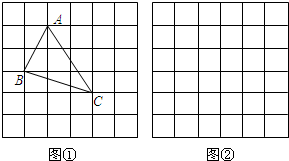
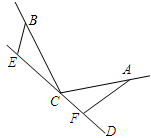 如图,直线CD经过∠BCA的顶点C,CA=CB,E,F分别是直线上CD上的两点,且∠BEC=∠CFA=∠α,如图,若直线CD经过∠BCA的外部,∠α=∠BCA,请探究EF与BE,AF三条线段的数量关系,并证明.
如图,直线CD经过∠BCA的顶点C,CA=CB,E,F分别是直线上CD上的两点,且∠BEC=∠CFA=∠α,如图,若直线CD经过∠BCA的外部,∠α=∠BCA,请探究EF与BE,AF三条线段的数量关系,并证明.