题目内容
把2016个正数1、2、3、4…,2016按如图的方式排列成一个表.
(1)如图,用一个正方形框在表中任意框住4个数,记左上角的一个数为x,则另外三个数用含x的式子从小到大依次表示为 , , .
(2)当被框住的4个数的和等于416时,x的值为多少?
(3)能否框住4个数,使它们的和等于324?如能,求出x的值;如不能,请说出理由.

(1)如图,用一个正方形框在表中任意框住4个数,记左上角的一个数为x,则另外三个数用含x的式子从小到大依次表示为
(2)当被框住的4个数的和等于416时,x的值为多少?
(3)能否框住4个数,使它们的和等于324?如能,求出x的值;如不能,请说出理由.

考点:一元一次方程的应用
专题:
分析:(1)左右相邻两个数差1,上下相邻的两个数相差为7,据此表示其他三个数;
(2)根据题意列出x+x+1+x+7+x+8=416,解一元一次方程求出x的值;
(3)令x+x+1+x+7+x+8=324,求出x的值,进而作出判断.
(2)根据题意列出x+x+1+x+7+x+8=416,解一元一次方程求出x的值;
(3)令x+x+1+x+7+x+8=324,求出x的值,进而作出判断.
解答:解:(1)由图表可知:左右相邻两个数差1,上下相邻的两个数相差为7,左上角的一个数为x,
则另外三个数用含x的式子从小到大依次表示x+1;x+7;x+8;
故答案为x+1;x+7;x+8;
(2)根据题意可得:x+x+1+x+7+x+8=416,
4x+16=416,
解得x=100,
答:x的值为100;
(3)假设x+x+1+x+7+x+8=324,
解得x=77,
答:能框住4个数,使它们的和等于324,x的值为77.
则另外三个数用含x的式子从小到大依次表示x+1;x+7;x+8;
故答案为x+1;x+7;x+8;
(2)根据题意可得:x+x+1+x+7+x+8=416,
4x+16=416,
解得x=100,
答:x的值为100;
(3)假设x+x+1+x+7+x+8=324,
解得x=77,
答:能框住4个数,使它们的和等于324,x的值为77.
点评:本题主要考查了一元一次方程组的应用,解答本题的关键是掌握上下每列两个数相差为7,此题难度不大.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
若
=
,则
为( )
| x-2y |
| 3y-x |
| 2 |
| 3 |
| y |
| x |
A、
| ||
B、
| ||
C、
| ||
D、-
|
已知等式3a=2b+5,则下列等式中,不一定成立的是( )
| A、3a-5=2b |
| B、3a-1=2b+4 |
| C、3ac=2b+5c |
| D、9a=6b+15 |
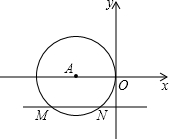 如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(-8,-4),则点N的坐标为
如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点,若点M的坐标是(-8,-4),则点N的坐标为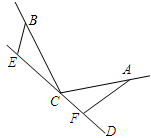 如图,直线CD经过∠BCA的顶点C,CA=CB,E,F分别是直线上CD上的两点,且∠BEC=∠CFA=∠α,如图,若直线CD经过∠BCA的外部,∠α=∠BCA,请探究EF与BE,AF三条线段的数量关系,并证明.
如图,直线CD经过∠BCA的顶点C,CA=CB,E,F分别是直线上CD上的两点,且∠BEC=∠CFA=∠α,如图,若直线CD经过∠BCA的外部,∠α=∠BCA,请探究EF与BE,AF三条线段的数量关系,并证明. 如图,已知在四边形ABCD中,AB=CD,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O.
如图,已知在四边形ABCD中,AB=CD,AD=BC,点E在BC上,点F在AD上,AF=CE,EF与对角线BD相交于点O.