题目内容
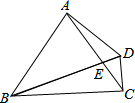 如图,△ABC是等边三角形,BD=AB,BD与AC交于点E,当点E在AC上运动时,∠ADC的大小是否发生变化?如果变化,请说明变化的范围,如果不变,请说明理由.
如图,△ABC是等边三角形,BD=AB,BD与AC交于点E,当点E在AC上运动时,∠ADC的大小是否发生变化?如果变化,请说明变化的范围,如果不变,请说明理由.考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:
分析:由等边三角形的性质就可以得出AB=AC=BC,∠ABC=60°,由BD=AB就可以得出BC=BD,就有∠4=∠ABD,∠3=∠BCD,由四边形的内角和就可以得出2∠3+2∠4+∠1+∠2=360°,就可以求出∠ADC的值而得出结论.
解答:解:∠ADC的大小不发生变化.
∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=60°.
∵BD=AB,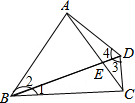
∴∠4=∠BAD,BD=BC,
∴∠3=∠BCD.
∵∠4+∠ABD+∠3+∠BCD+∠1+∠2=360°,
∴2∠3+2∠4+∠1+∠2=360°.
∵∠1+∠2=60°,
∴2∠3+2∠4+60°=360°,
∴∠3+∠4=150°,
即∠ADC=150°.
∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=60°.
∵BD=AB,

∴∠4=∠BAD,BD=BC,
∴∠3=∠BCD.
∵∠4+∠ABD+∠3+∠BCD+∠1+∠2=360°,
∴2∠3+2∠4+∠1+∠2=360°.
∵∠1+∠2=60°,
∴2∠3+2∠4+60°=360°,
∴∠3+∠4=150°,
即∠ADC=150°.
点评:本题考查了等边三角形的性质的运用,等腰三角形的性质的运用,四边形的内角和定理的运用,解答时灵活运用等边三角形的性质求解是关键.

练习册系列答案
相关题目
 如图,已知点B,E,C,F在一条直线上,并且△ABC≌△DEF,那么这两个全等三角形属于全等变换中的
如图,已知点B,E,C,F在一条直线上,并且△ABC≌△DEF,那么这两个全等三角形属于全等变换中的
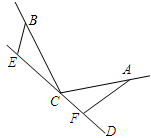 如图,直线CD经过∠BCA的顶点C,CA=CB,E,F分别是直线上CD上的两点,且∠BEC=∠CFA=∠α,如图,若直线CD经过∠BCA的外部,∠α=∠BCA,请探究EF与BE,AF三条线段的数量关系,并证明.
如图,直线CD经过∠BCA的顶点C,CA=CB,E,F分别是直线上CD上的两点,且∠BEC=∠CFA=∠α,如图,若直线CD经过∠BCA的外部,∠α=∠BCA,请探究EF与BE,AF三条线段的数量关系,并证明.