题目内容
2.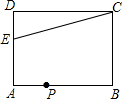 如图,在矩形ABCD中,E为AD上一点且AB=8,AE=3,BC=4,点P为AB边上一动点,若△PAE与△PBC是相似三角形,则AP=$\frac{24}{7}$或2或6.
如图,在矩形ABCD中,E为AD上一点且AB=8,AE=3,BC=4,点P为AB边上一动点,若△PAE与△PBC是相似三角形,则AP=$\frac{24}{7}$或2或6.
分析 设AP=x,则BP=8-x,分△PAE∽△PBC和△PAE∽△CBP两种情况,根据相似三角形的性质列出比例式,计算即可.
解答 解:设AP=x,则BP=8-x,
当△PAE∽△PBC时,$\frac{AE}{BC}$=$\frac{PA}{PB}$,即$\frac{3}{4}$=$\frac{x}{8-x}$,
解得,x=$\frac{24}{7}$,
当△PAE∽△CBP时,$\frac{AE}{PB}$=$\frac{PA}{BC}$,即$\frac{3}{8-x}$=$\frac{x}{4}$,
解得,x=2或6,
故答案为:$\frac{24}{7}$或2或6.
点评 本题考查了相似三角形的判定,掌握两组对应边的比相等且夹角对应相等的两个三角形相似是解题的关键,解答时,注意分情况讨论思想的灵活运用.

练习册系列答案
相关题目
10.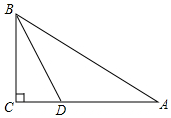 如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D.若CD=3cm,则点D到AB的距离DE是( )
如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D.若CD=3cm,则点D到AB的距离DE是( )
 如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D.若CD=3cm,则点D到AB的距离DE是( )
如图,Rt△ABC中,∠C=90°,∠ABC的平分线BD交AC于D.若CD=3cm,则点D到AB的距离DE是( )| A. | 5 cm | B. | 4 cm | C. | 3 cm | D. | 2 cm |
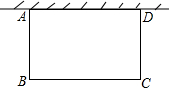 如图,一边靠学校院墙,其他三边用12m长的篱笆围成一个矩形花圃,设矩形ABCD的边AB=xm,面积为S m2.
如图,一边靠学校院墙,其他三边用12m长的篱笆围成一个矩形花圃,设矩形ABCD的边AB=xm,面积为S m2. 如图,⊙O是等腰三角形ABC的外接圆,AB=AC,∠A=45°,BD为⊙O的直径,连结CD,则∠DBA=22.5°.
如图,⊙O是等腰三角形ABC的外接圆,AB=AC,∠A=45°,BD为⊙O的直径,连结CD,则∠DBA=22.5°.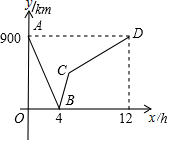 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x h,两车之间的距离为y km,如图所示的折线表示y与x之间的函数关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x h,两车之间的距离为y km,如图所示的折线表示y与x之间的函数关系.根据图象进行以下探究: