题目内容
12.已知关于x的二次函数y=ax2+2ax+a-3在-2≤x≤2时的函数值始终是负的,则常数a的取值范围是a<$\frac{1}{3}$且a≠0.分析 利用配方法求出抛物线的顶点坐标,根据二次函数的性质判断即可.
解答 解:y=ax2+2ax+a-3=a(x+1)2-3,
∴抛物线的顶点坐标为(-1,-3),
当a<0时,y<0,
当a>0时,由题意得,当x=2时,y<0,
即9a-3<0,
解得,a<$\frac{1}{3}$,
由二次函数的定义可知,a≠0,
故答案为:a<$\frac{1}{3}$且a≠0.
点评 本题考查的是二次函数图象上点的坐标特征,正确利用配方法把二次函数的一般式化为顶点式、掌握二次函数的性质是解题的关键.

练习册系列答案
相关题目
3.下列函数中自变量取值范围选取错误的是( )
| A. | y=$\frac{1}{x-1}$中x≠0 | B. | y=x2中x取全体实数 | ||
| C. | y=$\frac{1}{x+1}$中x≠-1 | D. | y=$\sqrt{x-1}$中x≥1 |
1.下列事件是必然事件的是( )
| A. | 2016年杨家坪房价一定下降 | |
| B. | 两个负数相乘,结果是正数 | |
| C. | 九龙坡区明天一定会下雪 | |
| D. | 小明努力学习,这次数学考试一定得满分 |
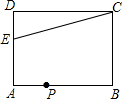 如图,在矩形ABCD中,E为AD上一点且AB=8,AE=3,BC=4,点P为AB边上一动点,若△PAE与△PBC是相似三角形,则AP=$\frac{24}{7}$或2或6.
如图,在矩形ABCD中,E为AD上一点且AB=8,AE=3,BC=4,点P为AB边上一动点,若△PAE与△PBC是相似三角形,则AP=$\frac{24}{7}$或2或6. 如图,∠AOC=30°35′15″,∠BOC=80°15′28″,OC平分∠AOD,那么∠BOD等于49°40′13″.
如图,∠AOC=30°35′15″,∠BOC=80°15′28″,OC平分∠AOD,那么∠BOD等于49°40′13″. 如图,△OAB是由△ODC绕点O逆时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为110°,求∠DOB的度数.
如图,△OAB是由△ODC绕点O逆时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为110°,求∠DOB的度数.