题目内容
17．
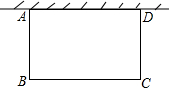如图，一边靠学校院墙，其他三边用12m长的篱笆围成一个矩形花圃，设矩形ABCD的边AB=xm，面积为S m2．（1）写出S与x之间的函数关系式；
（2）当x取何值时，面积S最大，最大值是多少？
分析 （1）根据矩形的面积公式可以写出S与x之间的函数关系式；
（2）将（1）中的函数关系式化为顶点式即可解答本题．
解答 解：（1）由题意可得，
S=x（12-2x）=-2x2+12x，
即S与x之间的函数关系式S=-2x2+12x；
（2）∵S=-2x2+12x=-2（x-3）2+18，
∴当x=3时，S取得最大值，此时S=18，
即当x=3时，面积S最大，最大值是18m2．
点评 本题考查二次函数的应用，解答此类问题的关键是明确题意，写出相应的函数关系式，利用函数的顶点式求函数的最值．
练习册系列答案
相关题目
如图，已知线段MN为正六边形ABCDEF平移后得到的一条边，请画出平移后的图形．
8．
如图，在⊙O中，弦AC=2$\sqrt{3}$ cm，C为⊙O上一点，且∠ABC=120°，则⊙O的直径为（ ）
如图，在⊙O中，弦AC=2$\sqrt{3}$ cm，C为⊙O上一点，且∠ABC=120°，则⊙O的直径为（ ）| A． | 2cm | B． | 4$\sqrt{3}$cm | C． | 4cm | D． | 6cm |
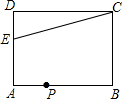如图，在矩形ABCD中，E为AD上一点且AB=8，AE=3，BC=4，点P为AB边上一动点，若△PAE与△PBC是相似三角形，则AP=$\frac{24}{7}$或2或6．