题目内容
12．已知y=ax2+bx+c中，当x=1时，y=0；当x=3时，y=0；当x=2时，y=2，则函数解析式为y=-2（x-1）（x-3）．分析 根据题意可设二次函数的解析式为y=a（x-1）（x-3），然后代入（2，2）利用待定系数法可求得a，从而求得函数的解析式．
解答 解：∵二次函数y=ax2+bx+c，过（1，0）（3，0）（2，2）三点，
∴设二次函数的解析式为y=a（x-1）（x-3），
代入（2，2）得，2=a（2-1）（2-3），
解得a=-2，
∴这个二次函数的解析式y=-2（x-1）（x-3）．
故答案为y=-2（x-1）（x-3）．
点评 本题考查了用待定系数法求二次函数的解析式，待定系数法是求函数解析式常用的方法，一定要熟练掌握．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
2．-1.5的倒数是（ ）
| A． | 0 | B． | -1.5 | C． | 1.5 | D． | -$\frac{2}{3}$ |
2．
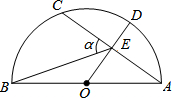如图，AB是半圆的直径，点O为圆心，OA=5，弦AC=8，OD⊥AC，垂足为E，交⊙O于点D，连接BE．设∠BEC=α，则sinα的值为（ ）
如图，AB是半圆的直径，点O为圆心，OA=5，弦AC=8，OD⊥AC，垂足为E，交⊙O于点D，连接BE．设∠BEC=α，则sinα的值为（ ）| A． | $\frac{3\sqrt{13}}{13}$ | B． | $\frac{2\sqrt{13}}{13}$ | C． | $\frac{\sqrt{13}}{13}$ | D． | $\frac{2}{3}$ |