题目内容
10．从长度分别是2，3，4的三条线段中随机抽出一条，与长为1，3的两条线段首尾顺次相接，能构成三角形的概率是（ ）| A． | 1 | B． | $\frac{2}{3}$ | C． | $\frac{1}{3}$ | D． | 0 |
分析 先写出3种等可能的结果数，然后根据三角形三边的关系确定三条线段能构成三角形的结果数，再根据概率公式求解．
解答 解：共有3种等可能的结果数，它们是：2、1、3，3、1、3，4、1、3，
其中三条线段能构成三角形的结果数为1，
所以三条线段能构成三角形的概率=$\frac{1}{3}$．
故选C．
点评 本题考查了概率公式：随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数．也考查了三角形三边的关系．
练习册系列答案
阅读快车系列答案
相关题目
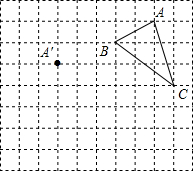在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示，现将△ABC平移，使点A变换为A′，点B′、C′分别是B、C的对应点．
如图，已知AF∥CD，AB∥DE，那么∠A=∠D吗？请说明理由．
如图，
如图，已知：AB∥CD，∠A=70°，∠DHE=70°，求证：AM∥EF．
给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称该四边形为勾股四边形．
19．
如图，在Rt△ABC中，∠C=90°，∠B=75°，将△ABC沿CD翻折，使点B落在边AC上的B′处，则BC：BD=（ ）
如图，在Rt△ABC中，∠C=90°，∠B=75°，将△ABC沿CD翻折，使点B落在边AC上的B′处，则BC：BD=（ ）| A． | $\sqrt{6}$：2 | B． | 3：2 | C． | $\sqrt{5}$：3 | D． | 5：3 |