��Ŀ����
5����֪������y=ax2+bx+c����ԭ��O����A��-4��0���͵�C��2��3����
��1���������ߵĽ���ʽ���������ꣻ
��2����ͼ1���������ߵĶԳ�����x�ύ�ڵ�E����ֱ��y=2x��y������ƽ��n����λ��õ�ֱ��l����ֱ��l����C�㣬��y�ύ�ڵ�D�����������ߵĶԳ��ύ�ڵ�F����P����������һ�㣬��PC=PF�����P�����ꣻ
��3����ͼ2������1������������������ƽ��4����λ�õ��������ߣ������������ϵ�ֱ��CD������̵ĵ�����꣮��ֱ��д���������Ҫ�����̣�
���� ��1�����ݴ���ϵ�������ɵú�������ʽ�������䷽�����ɵö��㼫���ꣻ
��2�����ݴ���ϵ�������ɵ�ֱ��l�Ľ���ʽ�������е����깫ʽ���ɵ�D��CF���е㣬���ݹ��ɶ������ɵ�EF��EC�������߶δ�ֱƽ���ߵ����ʣ��ɵ�ED���߶�CFֱƽ���ߣ����ݽⷽ���飬�ɵ�P�����ꣻ
��3������ƽ�ƣ��ɵ��������ߣ�����ƽ����ֱ�������������еĵ㵽ֱ�ߵľ�����̣��ɵ����ߣ����ݽⷽ���飬�ɵô𰸣�
��� ��1����������y=ax2+bx+c����ԭ��O����A��-4��0���͵�C��2��3����
��$\left\{\begin{array}{l}{c=0}\\{16a-4b+c=0}\\{4a+2b+c=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=\frac{1}{4}}\\{b=1}\\{c=0}\end{array}\right.$��
�������ߵĽ���ʽΪy=$\frac{1}{4}$x2+x��
��y=$\frac{1}{4}$x2+x=$\frac{1}{4}$��x+2��2-1��
�������ߵĶ�������Ϊ��-2��-1����
��2����ͼ1��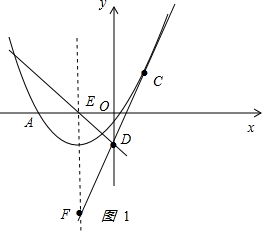
ֱ��l�Ľ���ʽΪy=2x-n��
��ֱ��l����C��2��3����
��n=1��
��ֱ��l�Ľ���ʽΪy=2x-1����x=0ʱ��y=-1����D��0��-1����
�������ߵĶԳ���Ϊx=-2��
��E��-2��0����
��x=-2ʱ��y=2x-1=-5����F��-2��-5����
��CD=DF=2$\sqrt{5}$��
���D���߶�CF���е㣬
��C��2��3����
��EF=EC=5��
��ED��ֱƽ��CF��
��PC=PF��
���P��CF�Ĵ�ֱƽ�����ϣ�
���P����������ֱ��ED�Ľ��㣮
ED�Ľ���ʽΪy=-$\frac{1}{2}$x-1��
������������ED����
$\left\{\begin{array}{l}{y=-\frac{1}{2}x-1}\\{y=\frac{1}{4}{x}^{2}+x}\end{array}\right.$��
���$\left\{\begin{array}{l}{{x}_{1}=-3+\sqrt{5}}\\{{y}_{1}=\frac{1-\sqrt{5}}{2}}\end{array}\right.$��$\left\{\begin{array}{l}{{x}_{2}=-3-\sqrt{5}}\\{{y}_{2}=\frac{1+\sqrt{5}}{2}}\end{array}\right.$��
��P�����꣨-3+$\sqrt{5}$��$\frac{1-\sqrt{5}}{2}$����-3-$\sqrt{5}$��$\frac{1+\sqrt{5}}{2}$����
��3����ͼ2��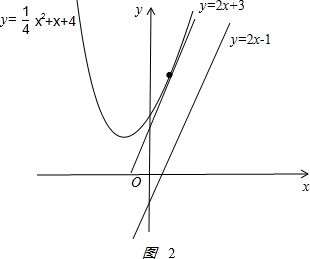
�ƺ��������Ϊy�T$\frac{1}{4}$x2+x+4
ƽ����CD���������е�ֱ��Ϊy=2x+b��
��������$\frac{1}{4}$x2+x+4=2x+b
��������ȶ�ʵ������
��=b2-4ac=��-1��2-4��$\frac{1}{4}$��4-b��=0
���b=3��
$\frac{1}{4}$x2-x+1=0��
���x=2��y=2x+3=7��
���������ϵ�ֱ��CD������̵ĵ�������ǣ�2��7����
���� ���⿼���˶��κ����ۺ��⣬���ô���ϵ������������ʽ�������߶δ�ֱƽ���ߵ����ʵó�P���߶�CD�Ĵ�ֱƽ�����������ߵĽ����ǽ���ؼ�������ƽ����ֱ�������������еĵ㵽ֱ�ߵľ�����̵ó������ߵ������ǽ���ؼ���

 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д� �ǽ�����ʱ��������Ż��⣬��������������Զ���ǽ�����һ����Ҫ��ʽ��Ϊ�˽�ij�г���ѧ��ÿ���������������ʱ��������������������100������ѧ�������ݵ������õ���ͼ��ʾ��ͳ��ͼ����
�ǽ�����ʱ��������Ż��⣬��������������Զ���ǽ�����һ����Ҫ��ʽ��Ϊ�˽�ij�г���ѧ��ÿ���������������ʱ��������������������100������ѧ�������ݵ������õ���ͼ��ʾ��ͳ��ͼ����| ��� | ʱ��t��Сʱ�� | ���� |
| A | t��0.5 | 5 |
| B | 0.5��t��1 | 20 |
| C | 1��t��1.5 | a |
| D | 1.5��t��2 | 30 |
| E | t��2 | 10 |
��2����ȫ����ͳ��ͼ��
��3�����˽���д�Լ��30��������ѧ��������Ƹ��г���ѧ��ÿ�������������ʱ����1Сʱ���ϵ�������
 ����ͼ���У���ͼ��ʾ������ĸ���ͼ���ǣ�������
����ͼ���У���ͼ��ʾ������ĸ���ͼ���ǣ�������| A�� |  | B�� |  | C�� |  | D�� |  |
| A�� | 1 | B�� | $\frac{2}{3}$ | C�� | $\frac{1}{3}$ | D�� | 0 |
| A�� | ���dz������ڲ��dz��� | B�� | ���Dz����������dz��� | ||
| C�� | �١��ڶ��dz��� | D�� | �١��ڶ����dz��� |

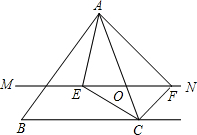 �ڡ�ABC�У���O��AC���ϵ�һ�㣬����O��ֱ��MN��BC����MN����BCA��ƽ�����ڵ�E������BCA����ǵ�ƽ�����ڵ�F������AE��AF��
�ڡ�ABC�У���O��AC���ϵ�һ�㣬����O��ֱ��MN��BC����MN����BCA��ƽ�����ڵ�E������BCA����ǵ�ƽ�����ڵ�F������AE��AF��