题目内容
4．已知直线y=mx与双曲线y=$\frac{k}{x}$的一个交点A的坐标为（-1，-2），则直线的解析式为y=2x，双曲线的解析式为y=$\frac{2}{x}$．分析 把（-1，-2）代入y=mx与双曲线y=$\frac{k}{x}$可得m、k的值，进而可得答案．
解答 解：∵直线y=mx与双曲线y=$\frac{k}{x}$的一个交点A的坐标为（-1，-2），
∴2=m×1，-2=$\frac{k}{-1}$，
∴2=m，k=2，
∴直线的解析式为y=2x，双曲线的解析式为y=$\frac{2}{x}$，
故答案为：y=2x；y=$\frac{2}{x}$．
点评 此题主要考查了反比例函数与一次函数的交点，关键是掌握凡是函数图象经过的点必能满足解析式．
练习册系列答案
备战中考寒假系列答案
相关题目
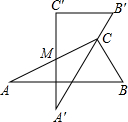如图是两块完全一样的含30°角的直角三角板，将它们重叠在一起并绕其较长直角边的中点M转动，使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C．已知AC=5，则这块直角三角板顶点A、A′之间的距离等于2.5．
12．将抛物线y=x2+5向右平移1个单位长度，再向下平移2个单位长度，后，得到的抛物线解析式是（ ）
| A． | y=（x-1）2+3 | B． | y=（x+1）2+3 | C． | y=（x+1）2-3 | D． | y=（x-1）2-3 |
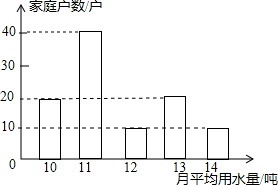为了倡导“节约用水，从我做起”，某市政府决定对市直机关600户家庭的用水情况作一次调查，市政府调查小组随机抽查了其中的100户家庭去年一年的月平均用水量（单位：吨），并将调查结果制成了如图所示的条形统计图．
如图，在正方形ABCD中，AC与BD相交于点O，E为AD上的一点，连接BE，点G在BE上，连结OG并延长交AD于点F，若∠FGE=45°．
14．下列计算中正确的是（ ）
| A． | $\sqrt{m^2}+\sqrt{n^2}=\sqrt{{m^2}+{n^2}}$ | B． | $\sqrt{{a^2}-{b^2}}=\sqrt{a^2}-\sqrt{b^2}=a-b$ | ||
| C． | $\sqrt{3}×\sqrt{2}=\sqrt{3×2}$ | D． | $\sqrt{{{（{-3}）}^2}}=-3$ |