题目内容
6.已知(22n)2•(4n)4•84=1,则32n的值为$\frac{1}{9}$.分析 先把等式左边的式子写成底数为2的幂的形式后再通过幂的乘法和幂的乘方运算,计算得到底数为2的幂,再根据指数相等可得n的值,代入计算即可.
解答 解:∵(22n)2•(4n)4•84=24n•(22)4n•(23)4
=24n•28n•212
=212n+12=1,
∴12n+12=0,解得:n=-1,
∴32n=3-2=$\frac{1}{{3}^{2}}=\frac{1}{9}$,
故答案为:$\frac{1}{9}$.
点评 本题主要考查幂的运算能力,掌握同底数幂的乘法运算(底数不变指数相加)和幂的乘方运算(底数不变指数相乘)及负指数幂是根本.

练习册系列答案
相关题目
17.已知一个等腰三角形的两条边长分别为3和8,则这个等腰三角形的周长为( )
| A. | 11 | B. | 14 | C. | 19 | D. | 14或19 |
14.下列计算中正确的是( )
| A. | $\sqrt{m^2}+\sqrt{n^2}=\sqrt{{m^2}+{n^2}}$ | B. | $\sqrt{{a^2}-{b^2}}=\sqrt{a^2}-\sqrt{b^2}=a-b$ | ||
| C. | $\sqrt{3}×\sqrt{2}=\sqrt{3×2}$ | D. | $\sqrt{{{({-3})}^2}}=-3$ |
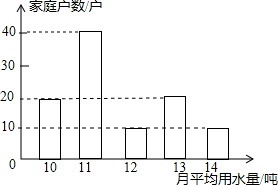 为了倡导“节约用水,从我做起”,某市政府决定对市直机关600户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭去年一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.
为了倡导“节约用水,从我做起”,某市政府决定对市直机关600户家庭的用水情况作一次调查,市政府调查小组随机抽查了其中的100户家庭去年一年的月平均用水量(单位:吨),并将调查结果制成了如图所示的条形统计图.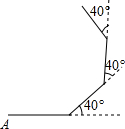 如图,小明在操场上从A点出发,沿直线前进10米后向左转40°,再沿直线前进10米后,又向左转40°,照这样走下去,他第一次回到出发地A点时,一共走了( )米.
如图,小明在操场上从A点出发,沿直线前进10米后向左转40°,再沿直线前进10米后,又向左转40°,照这样走下去,他第一次回到出发地A点时,一共走了( )米.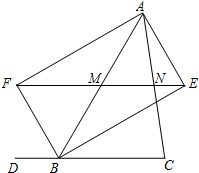 已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N.求证:
已知:如图,BE、BF分别是∠ABC与它的邻补角∠ABD的平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F,EF分别交边AB、AC于点M和N.求证: 已知如图,在?ABCD中,BF⊥AD、BE⊥DC,垂足分别是F、E,∠EDF=30°,BE=8,BF=14,则?ABCD的周长是88.
已知如图,在?ABCD中,BF⊥AD、BE⊥DC,垂足分别是F、E,∠EDF=30°,BE=8,BF=14,则?ABCD的周长是88.