题目内容
如图，△ABC的顶点是边长为1的正方形网格的格点，（1）直接写出cosB和tan（∠ACB-90°）的值；
（2）求sinA的值．
考点：解直角三角形
专题：网格型
分析：利用网格构造直角三角形，根据锐角三角函数的定义解答．
解答：
解：（1）如图，过点A作AF⊥BC于F，AE⊥CE于E．
在直角△ABF中，cosB=
=
=
；
在直角△ACE中，tan（∠ACB-90°）=tan∠ACE=
=
；
（2）如图，过点C作CD⊥AB于D，
∵S△ABC=
CD×AB=
BC×AF，
∴CD×AB=BC×AF，
∴CD×3
=2×3，
∴CD=
，
在Rt△ADC中，sinA=
=
=
．
解：（1）如图，过点A作AF⊥BC于F，AE⊥CE于E．在直角△ABF中，cosB=
| BF |
| AB |
| 3 | ||
3
|
| ||
| 2 |
在直角△ACE中，tan（∠ACB-90°）=tan∠ACE=
| AE |
| CE |
| 1 |
| 3 |
（2）如图，过点C作CD⊥AB于D，
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CD×AB=BC×AF，
∴CD×3
| 2 |
∴CD=
| 2 |
在Rt△ADC中，sinA=
| CD |
| AC |
| ||
|
| ||
| 5 |
点评：本题考查了锐角三角函数的定义和勾股定理，作出辅助线并利用网格构造直角三角形是解题的关键．
练习册系列答案
习题精选系列答案
相关题目
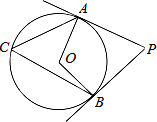如图，AP、BP分别切⊙O于点A、B，∠P=60°，点C是圆上一动点，则∠C的度数为（ ）| A、60 | B、40 |
| C、72° | D、60°或120° |
在如图直角坐标系中，已知A（0，a），B（b，0），C（b，c）三点，其中a、b、c满足关系式