题目内容
 在如图直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式
在如图直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式| a-2 |
(1)求a、b、c的值;
(2)如果点P(m,n)在第二象限,四边形CBOP的面积为y,请你用含m,n的式子表示y;
(3)如果点P在第二象限坐标轴的夹角平分线上,并且y=2S四边形CBOA,求P点的坐标.
考点:坐标与图形性质,非负数的性质:偶次方,非负数的性质:算术平方根,三角形的面积
专题:
分析:(1)利用二次根式的性质以及绝对值的性质得出a,b,c的值即可;
(2)利用四边形面积求法,将原图形分割,进而得出即可;
(3)利用(2)中所求,再结合角平分线的性质以及第二象限点的坐标性质得出答案即可.
(2)利用四边形面积求法,将原图形分割,进而得出即可;
(3)利用(2)中所求,再结合角平分线的性质以及第二象限点的坐标性质得出答案即可.
解答:解:(1)∵
+(b-3)2=0,(c-4)2≤0,
∴a=2,b=3,c=4;
(2)∵点P(m,n)在第二象限,四边形CBOP的面积为y,
∴y=
×(AO+BC)×BO+
(-m)n=9-
;
(3)∵点P在第二象限坐标轴的夹角平分线上,且y=2S四边形CBOA,
∴-m=n,且y=2S四边形CBOA=2×9=18,
∴9-
=18,
即9+
n2=18,
解得:n=±3
,
∵点P在第二象限,
∴n>0,
∴P点的坐标为:(-3
,3
).
| a-2 |

∴a=2,b=3,c=4;
(2)∵点P(m,n)在第二象限,四边形CBOP的面积为y,
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| mn |
| 2 |
(3)∵点P在第二象限坐标轴的夹角平分线上,且y=2S四边形CBOA,
∴-m=n,且y=2S四边形CBOA=2×9=18,
∴9-
| mn |
| 2 |
即9+
| 1 |
| 2 |
解得:n=±3
| 2 |
∵点P在第二象限,
∴n>0,
∴P点的坐标为:(-3
| 2 |
| 2 |
点评:此题主要考查了图形面积求法以及坐标性质和角平分线的性质等知识,正确分割四边形求出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC的顶点是边长为1的正方形网格的格点,
如图,△ABC的顶点是边长为1的正方形网格的格点,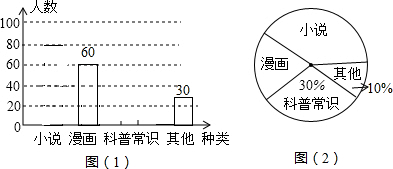
 如图,在△ABC和△CDE中,∠ACB=∠DCE=90°,AC=BC,DC=EC,且点A在CD上,连接AE、BD.
如图,在△ABC和△CDE中,∠ACB=∠DCE=90°,AC=BC,DC=EC,且点A在CD上,连接AE、BD.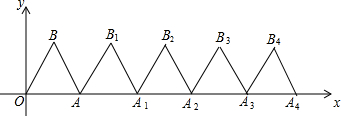 如图,△ABO是边长为6的等边三角形,将△ABO向右平移得第2个等边三角形△A1B1A;再将△A1B1A向右平移得第3个等边三角形△A2B2A1,重复以上做法得到第5个等边三角形△A4B4A3,若P(m,2
如图,△ABO是边长为6的等边三角形,将△ABO向右平移得第2个等边三角形△A1B1A;再将△A1B1A向右平移得第3个等边三角形△A2B2A1,重复以上做法得到第5个等边三角形△A4B4A3,若P(m,2 如图为等边三角形ABC和正方形DEFG的重叠情形,其中D,E两点分别在BC,AC上,且CD=CE.若AB=6,GF=2,则点F到AB的距离是
如图为等边三角形ABC和正方形DEFG的重叠情形,其中D,E两点分别在BC,AC上,且CD=CE.若AB=6,GF=2,则点F到AB的距离是