题目内容
已知:关于x的方程x2+(2m+4)x+m2+5m没有实数根.
(1)求m的取值范围;
(2)若关于x的一元二次方程mx2+(n-2)x+m-3=0有实数根,求证:该方程两根的符号相同;
(3)设(2)中方程的两根分别为α、β,若α:β=1:2,且n为整数,求m的最小整数值.
(1)求m的取值范围;
(2)若关于x的一元二次方程mx2+(n-2)x+m-3=0有实数根,求证:该方程两根的符号相同;
(3)设(2)中方程的两根分别为α、β,若α:β=1:2,且n为整数,求m的最小整数值.
考点:根的判别式,根与系数的关系
专题:
分析:(1)根据一元二次方程根的情况与判别式△的关系:△>0?方程有两个不相等的实数根;△=0?方程有两个相等的实数根;△<0?方程没有实数根,代入计算即可得出答案;
(2)根据由于方程mx2+(n-2)x+m-3=0有两个实数根可知m≠0,当m>4时,得出两根的积
>0,从而得出方程的两根符号相同;
(3)由已知得m≠0,α+β=-
,α•β=
,再根据α:β=1:2,得出3α=-
,2a2=
,再进行整理得出(n-2)2=
m(m-3),根据m>4,且n为整数,得出m为整数,即可得出答案.
(2)根据由于方程mx2+(n-2)x+m-3=0有两个实数根可知m≠0,当m>4时,得出两根的积
| m-3 |
| m |
(3)由已知得m≠0,α+β=-
| n-2 |
| m |
| m-3 |
| m |
| n-2 |
| m |
| m-3 |
| m |
| 9 |
| 2 |
解答:解:(1)∵关于x的方程x2+(2m+4)x+m2+5m没有实数根,
∴△=(2m+4)2-4×1×(m2+5m)<0,
∴m>4,
∴m的取值范围是m>4;
(2)由于方程mx2+(n-2)x+m-3=0有两个实数根可知m≠0,
当m>4时,
>0,即方程的两根之积为正,
故方程的两根符号相同.
(3)由已知得:m≠0,α+β=-
,α•β=
.
∵α:β=1:2,
∴3α=-
,2a2=
.
=
,即(n-2)2=
m(m-3).
∵m>4,且n为整数,
∴m为整数;
当m=6时,(n-2)2=
×6×3=81.
∴m的最小值为6.
∴△=(2m+4)2-4×1×(m2+5m)<0,
∴m>4,
∴m的取值范围是m>4;
(2)由于方程mx2+(n-2)x+m-3=0有两个实数根可知m≠0,
当m>4时,
| m-3 |
| m |
故方程的两根符号相同.
(3)由已知得:m≠0,α+β=-
| n-2 |
| m |
| m-3 |
| m |
∵α:β=1:2,
∴3α=-
| n-2 |
| m |
| m-3 |
| m |
| (n-2)2 |
| 9m2 |
| m-3 |
| 2m |
| 9 |
| 2 |
∵m>4,且n为整数,
∴m为整数;
当m=6时,(n-2)2=
| 9 |
| 2 |
∴m的最小值为6.
点评:此题考查了根的判别式以及根与系数的关系,一元二次方程根的情况与判别式△的关系:△>0?方程有两个不相等的实数根;△=0?方程有两个相等的实数根;△<0?方程没有实数根.

练习册系列答案
相关题目
若二次函数f(x)=ax2+bx+c的对称轴为x=1,且其图象过点(2,0),则
的值是( )
| f(-1) |
| f(1) |
| A、-3 | B、-2 | C、2 | D、3 |

 如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF;
如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF;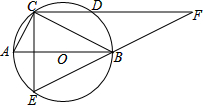 如图,⊙O上两点C、E关于直径AB对称,连接AC、BC,过C作CE的垂线,交⊙O于点D,交EB的延长线交于点F,且BC:CA=
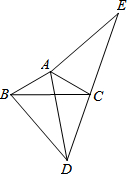
如图,⊙O上两点C、E关于直径AB对称,连接AC、BC,过C作CE的垂线,交⊙O于点D,交EB的延长线交于点F,且BC:CA= 如图,△ABC的顶点是边长为1的正方形网格的格点,
如图,△ABC的顶点是边长为1的正方形网格的格点,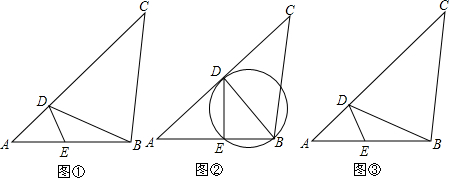
 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点C在DE上.求证:
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点C在DE上.求证: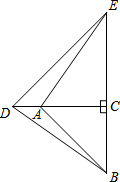 如图,在△ABC和△CDE中,∠ACB=∠DCE=90°,AC=BC,DC=EC,且点A在CD上,连接AE、BD.
如图,在△ABC和△CDE中,∠ACB=∠DCE=90°,AC=BC,DC=EC,且点A在CD上,连接AE、BD.