题目内容
某中学计划购买A,B两种型号的课桌凳,已知一套A型课桌凳比一套B型课桌凳少40元,且购买5套A型和1套B型共需1000元.
(1)购买一套A型课桌凳和一套B型课桌凳各需要多少元?
(2)学校根据实际情况计划购买A,B两种型号的共100套,且购买课桌凳的总费用不超过18480元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
(1)购买一套A型课桌凳和一套B型课桌凳各需要多少元?
(2)学校根据实际情况计划购买A,B两种型号的共100套,且购买课桌凳的总费用不超过18480元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的
| 2 |
| 3 |
考点:一元一次不等式组的应用,二元一次方程组的应用
专题:
分析:(1)设购买一套A型课桌凳需要x元,则一套B型为(x+40)元,根据购买5套A型和1套B型共需1000元可列方程求解.
(2)设购买A型课桌凳m套,则购买B型课桌凳(100-m)套,根据购买课桌凳的总费用不超过18480元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的
,可列不等式组求解.
(2)设购买A型课桌凳m套,则购买B型课桌凳(100-m)套,根据购买课桌凳的总费用不超过18480元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的
| 2 |
| 3 |
解答:解:(1)设一套A型课桌凳需要x元,则一套B型为(x+40)元,依题意有
5x+(x+40)=1000,
解得x=160,
x+40=200,
故购买一套A型课桌凳需要160元,一套B型课桌凳各需要200元.
(2)设购买A型课桌凳m套,则购买B型课桌凳(100-m)套,依题意有
,
解得38≤m≤40,
∵m为整数,
∴m为38或39或40.
当m=38时,100-m=62,总费用为160×38+200×62=6080+12400=18480(元);
当m=39时,100-m=61,总费用为160×39+200×61=6240+12200=18440(元);
当m=40时,100-m=60,总费用为160×40+200×60=6400+12000=18400(元);
所以该校本次购买A型和B型课桌凳共有3种方案,购买A型课桌凳40套,则购买B型课桌凳60套方案的总费用最低.
5x+(x+40)=1000,
解得x=160,
x+40=200,
故购买一套A型课桌凳需要160元,一套B型课桌凳各需要200元.
(2)设购买A型课桌凳m套,则购买B型课桌凳(100-m)套,依题意有
|
解得38≤m≤40,
∵m为整数,
∴m为38或39或40.
当m=38时,100-m=62,总费用为160×38+200×62=6080+12400=18480(元);
当m=39时,100-m=61,总费用为160×39+200×61=6240+12200=18440(元);
当m=40时,100-m=60,总费用为160×40+200×60=6400+12000=18400(元);
所以该校本次购买A型和B型课桌凳共有3种方案,购买A型课桌凳40套,则购买B型课桌凳60套方案的总费用最低.
点评:本题考查理解题意的能力,关键根据购买课桌凳数不同钱数的不同求出购买课桌凳的钱数,然后要求购买的总费用不超过18480元,并且购买A型课桌凳的数量不能超过B型课桌凳数量的
,列出不等式组求解.
| 2 |
| 3 |

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
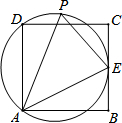 如图,已知在边长为8的正方形ABCD中,E是BC边的中点,P在过A、E、D三点的圆上,则△APE面积的最大值是( )
如图,已知在边长为8的正方形ABCD中,E是BC边的中点,P在过A、E、D三点的圆上,则△APE面积的最大值是( )A、10
| ||
B、10
| ||
| C、32 | ||
D、5
|
 如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF;
如图,点C、E、B、F在同一直线上,AC∥DF,AC=DF,BC=EF; 如图,△ABC的顶点是边长为1的正方形网格的格点,
如图,△ABC的顶点是边长为1的正方形网格的格点,
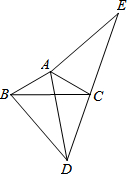 如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点C在DE上.求证:
如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,点C在DE上.求证:
 如图,△ABO是边长为6的等边三角形,将△ABO向右平移得第2个等边三角形△A1B1A;再将△A1B1A向右平移得第3个等边三角形△A2B2A1,重复以上做法得到第5个等边三角形△A4B4A3,若P(m,2
如图,△ABO是边长为6的等边三角形,将△ABO向右平移得第2个等边三角形△A1B1A;再将△A1B1A向右平移得第3个等边三角形△A2B2A1,重复以上做法得到第5个等边三角形△A4B4A3,若P(m,2