题目内容
17.已知平行四边形ABCD的周长为42,自顶点D作DE⊥AB于E,DF⊥BC于F,若DE=3,DF=4,则BE+BF的长为( )| A. | 21-14$\sqrt{2}$ | B. | 21+14$\sqrt{2}$ | C. | 21+14$\sqrt{2}$或21-14$\sqrt{2}$ | D. | 3+2$\sqrt{2}$或21+14$\sqrt{2}$ |
分析 根据∠A为锐角或∠D为锐角分情况进行讨论,由?ABCD的周长为42,DE⊥直线BC,DF⊥直线AB,垂足分别为E、F,且DE=3,DF=4,构造方程求解即可求得答案.
解答 解:对于平行四边形ABCD有两种情况: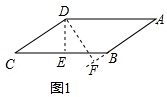
当∠A为锐角时,如图1,
设BC=a,AB=b,
∵平行四边形ABCD,DE⊥AB,DF⊥BC,
∴AB×DE=BC×DF,AB=CD,BC=DA,
又∵DE=3,DF=4,
∴3a=4b,
∵平行四边形ABCD的周长为42,
∴2(a+b)=42,
∴a+b=21,
则$\left\{\begin{array}{l}{3a=4b①}\\{a+b=21②}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=12}\\{b=9}\end{array}\right.$,
∴BC=12,AB=9,
∴AB=CD=9,AD=BC=12,
∴在Rt△ADE中,CE=6$\sqrt{2}$,
∴BE=BC-CE=12-6$\sqrt{2}$,
∴在Rt△ADF中,AF=8$\sqrt{2}$,
∵F点在AB的延长线上,
∴BF=AF-AB=8$\sqrt{2}$-9,
∴BE+BF=(12-6$\sqrt{2}$)+(8$\sqrt{2}$-9)=3+2$\sqrt{2}$,
当∠D为锐角时,如图2,
设BC=a,AB=b,
∵平行四边形ABCD,DE⊥AB,DF⊥BC,
∴AB×DE=BC×DF,AB=CD,BC=DA,
又∵DE=3,DF=4,
∴3a=4b,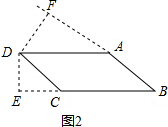
∵平行四边形ABCD的周长为28,
∴2(a+b)=42,
∴a+b=21,
解方程组$\left\{\begin{array}{l}{3a=4b①}\\{a+b=21②}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=12}\\{b=9}\end{array}\right.$,
∴BC=12,AB=9,
∴AB=CD=9,AD=BC=12,
∴在Rt△ADE中,CE=6$\sqrt{2}$,
∴BE=BC+CE=12+6$\sqrt{2}$,
∴在Rt△ADF中,AF=8$\sqrt{2}$,
∵F点在AB的延长线上,
∴BF=AF+AB=8$\sqrt{2}$+9,
∴BE+BF=(12+6$\sqrt{2}$)+(8$\sqrt{2}$+9)=14$\sqrt{2}$+21,
综上所述:BE+BF的长为:3+2$\sqrt{2}$或21+14$\sqrt{2}$.
故选:D.
点评 本题主要考查平行四边形的性质,勾股定理,合并同类二次根式等知识点,关键在于根据∠A为锐角或∠D为锐角分情况进行讨论,根据平行四边形的面积公式和周长定理正确的列出方程组,并认真的求解,推出AB和BC的长度,熟练运用数形结合的思想进行求解.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案①32-4×12=5;②52-4×22=9;③72-4×32=13;…
根据上述式子的规律,解答下列问题:
(1)第④个等式为92-4×42=17;
(2)写出第n个等式,并说明其正确性.
| A. | $\sqrt{3}$+$\sqrt{7}$=$\sqrt{10}$ | B. | 7$\sqrt{7}$-2$\sqrt{2}$=5$\sqrt{5}$ | C. | 2$\sqrt{2}$×3$\sqrt{2}$=6$\sqrt{2}$ | D. | $\sqrt{2}$÷$\sqrt{5}$=$\frac{\sqrt{10}}{5}$ |
| A. | 掷一枚硬币,正面朝上 | |
| B. | 从2、4、6、8、10这5张卡片中任抽一张是奇数 | |
| C. | a是实数,|a|≥0 | |
| D. | 从车间刚生产的产品中任意抽取一件,是次品 |
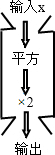 如图是一组数值转换机,若它输出的结果为32,则输入值为( )
如图是一组数值转换机,若它输出的结果为32,则输入值为( )| A. | ±8 | B. | 8 | C. | ±4 | D. | 4 |
 如图,①如果AD∥BC,那么根据两直线平行,同旁内角互补,得∠BAD+∠ABC=180°;②如果AB∥CD,那么根据两直线平行,同旁内角互补,得∠BCD+∠ABC=180°.
如图,①如果AD∥BC,那么根据两直线平行,同旁内角互补,得∠BAD+∠ABC=180°;②如果AB∥CD,那么根据两直线平行,同旁内角互补,得∠BCD+∠ABC=180°. 如图,在△ABC中,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、补角∠ACF,下列结论:①AD∥BC;②∠ACB=2∠ADB;③∠DCF=∠BDC+∠ABD;④∠BDC=∠BAC,其中正确的结论有( )
如图,在△ABC中,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、补角∠ACF,下列结论:①AD∥BC;②∠ACB=2∠ADB;③∠DCF=∠BDC+∠ABD;④∠BDC=∠BAC,其中正确的结论有( )