题目内容
15.已知三角形的两边分别是2cm和4cm,现从长度分别为2cm、3cm、4cm、5cm、6cm五根小木棒中随机抽一根,抽到的木棒能作为该三角形第三边的概率是$\frac{3}{5}$.分析 根据三角形三边的关系确定三角形第三边的取值范围,然后根据概率公式求解.
解答 解:∵三角形的两边分别是2cm和4cm,
∴第三边取值为大于2cm小于6cm,
∴2cm、3cm、4cm、5cm、6cm五根小木棒中3cm、4cm、5cm三根小棒满足条件,
∴抽到的木棒能作为该三角形第三边的概率为$\frac{3}{5}$,
故答案为$\frac{3}{5}$.
点评 本题考查了概率公式:随机事件A的概率P(A)=事件A可能出现的结果数除以所有可能出现的结果数.也考查了三角形三边的关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.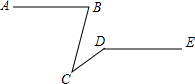 如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )
如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )
 如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )
如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )| A. | 20° | B. | 30° | C. | 40° | D. | 70° |
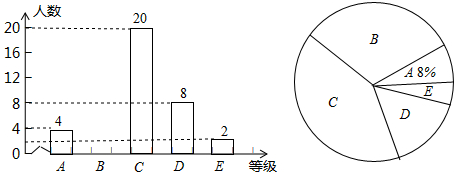
3.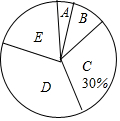 为了了解某校九年级(1)班学生的体育测试情况,对全班学生的体育成绩进行了统计,并绘制出以下不完整的频数分布表和扇形统计图
为了了解某校九年级(1)班学生的体育测试情况,对全班学生的体育成绩进行了统计,并绘制出以下不完整的频数分布表和扇形统计图
(1)求全班学生人数和m的值;
(2)该班学生的体育成绩的中位数落在哪个分数段内?
(3)该班体育成绩满分(60分)共有3人,其中男生2人,女生1人,现从这3人中随机选取2人参加校运动会,求恰好选到一男一女生的概率
 为了了解某校九年级(1)班学生的体育测试情况,对全班学生的体育成绩进行了统计,并绘制出以下不完整的频数分布表和扇形统计图
为了了解某校九年级(1)班学生的体育测试情况,对全班学生的体育成绩进行了统计,并绘制出以下不完整的频数分布表和扇形统计图(1)求全班学生人数和m的值;
(2)该班学生的体育成绩的中位数落在哪个分数段内?
(3)该班体育成绩满分(60分)共有3人,其中男生2人,女生1人,现从这3人中随机选取2人参加校运动会,求恰好选到一男一女生的概率
| 分组 | 分数段(分) | 频数 |
| A | 36≤x<41 | 2 |
| B | 41≤x<46 | 5 |
| C | 46≤x<51 | 15 |
| D | 51≤x<56 | m |
| E | 56≤x<61 | 10 |
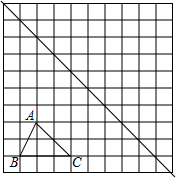 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)及直线l.
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点)及直线l.