题目内容
5.设抛物线y=x2-x-1与x轴的两交点为A,B,则线段AB的长为$\sqrt{5}$.分析 先求出抛物线与x轴的交点坐标,即可得出答案.
解答 解:当y=0时,x2-x-1=0,
解得:x=$\frac{1±\sqrt{5}}{2}$,
∴线段AB=$\frac{1+\sqrt{5}}{2}$-$\frac{1-\sqrt{5}}{2}$=$\sqrt{5}$,
故答案为:$\sqrt{5}$.
点评 本题考查了抛物线与x轴的交点问题,能求出A、B的坐标是解此题的关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
14.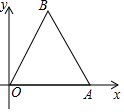 如图,等边△OAB的边长为2,则点B的坐标为( )
如图,等边△OAB的边长为2,则点B的坐标为( )
 如图,等边△OAB的边长为2,则点B的坐标为( )
如图,等边△OAB的边长为2,则点B的坐标为( )| A. | (1,1) | B. | ($\sqrt{3}$,1) | C. | ($\sqrt{3}$,$\sqrt{3}$) | D. | (1,$\sqrt{3}$) |
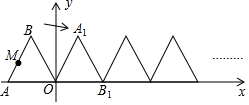 如图,正△ABO的边长为2,O为坐标原点,A在x轴上,B在第二象限,△ABO沿x轴正方向作无滑动的翻滚,经一次翻滚后得到△A1B1O,则翻滚3次后点B的对应点的坐标是(5,$\sqrt{3}$),翻滚2017次后AB中点M经过的路径长为($\frac{1346\sqrt{3}}{3}$+896)π.
如图,正△ABO的边长为2,O为坐标原点,A在x轴上,B在第二象限,△ABO沿x轴正方向作无滑动的翻滚,经一次翻滚后得到△A1B1O,则翻滚3次后点B的对应点的坐标是(5,$\sqrt{3}$),翻滚2017次后AB中点M经过的路径长为($\frac{1346\sqrt{3}}{3}$+896)π.