Question

6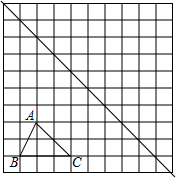．如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点）及直线l．
（1）画出△ABC关于直线l对称的△A₁B₁C₁；
（2）将△A₁B₁C₁绕点A₁按顺时针旋转90°得到△A₂B₂C₂，画出△A₂B₂C₂，并求出旋转过程中线段A₁C₁扫过的区域面积S．

Answer 1

分析 （1）分别作出△ABC的三顶点关于直线l对称的对应点，顺次连接即可得；
（2）分别作出△A₁B₁C₁三顶点绕点A₁按顺时针旋转90°得到对应点，顺次连接即可得，由扇形的面积公式可得答案．

解答 解：（1）如图所示，△A₁B₁C₁即为所求；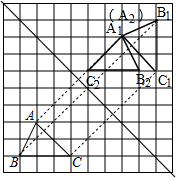


（2）如图所示，△A₂B₂C₂即为所求，
∵A₁C₁=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$，
则线段A₁C₁扫过的区域面积S=$\frac{90•π•（2\sqrt{2}）^{2}}{360}$=2π．

点评 本题主要考查作图-轴对称变换和旋转变换及扇形的面积公式，熟练掌握轴对称变换和旋转变换的定义和性质是解题的关键．