题目内容
5.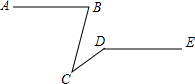 如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )
如图,已知AB∥DE,∠ABC=75°,∠CDE=145°,则∠BCD的值为( )| A. | 20° | B. | 30° | C. | 40° | D. | 70° |
分析 延长ED交BC于F,根据平行线的性质求出∠MFC=∠B=75°,求出∠FDC=35°,根据三角形外角性质得出∠C=∠MFC-∠MDC,代入求出即可.
解答 解:延长ED交BC于F,如图所示:
∵AB∥DE,∠ABC=75°,
∴∠MFC=∠B=75°,
∵∠CDE=145°,
∴∠FDC=180°-145°=35°,
∴∠C=∠MFC-∠MDC=75°-35°=40°,
故选C.
点评 本题考查了三角形外角性质,平行线的性质的应用,解此题的关键是求出∠MFC的度数,注意:两直线平行,同位角相等.

练习册系列答案
相关题目
20.小华进行了5次射击训练后,计算出这5次射击的平均成绩为8环,方差为s12,随后小华又进行了第6次射击,成绩恰好是8环,并计算出这6此射击成绩的方差为s22,则下列说法正确的是( )
| A. | s12=s22 | B. | s12<s22 | ||
| C. | s12>s22 | D. | 无法确定s12与s22的大小 |
17.若二次函数y=-x2+4x+c的图象经过A(1,y1),B(-1,y2),C(2+$\sqrt{2}$,y3)三点,则y1、y2、y3的大小关系是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y2<y3<y1 | D. | y2<y1<y3 |
 已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空).
已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空).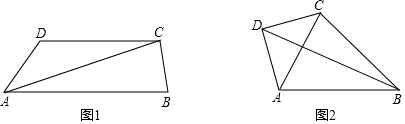
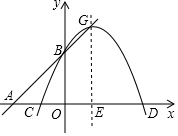 已知二次函数y=ax2-4ax+a2+2(a<0)图象的顶点G在直线AB上,其中
已知二次函数y=ax2-4ax+a2+2(a<0)图象的顶点G在直线AB上,其中