题目内容
9.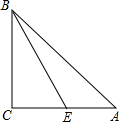 已知:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,点E是AC边上的一个动点(点E与点A、C不重合).
已知:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,点E是AC边上的一个动点(点E与点A、C不重合).(1)当a、b满足a2+b2-16a-12b+100=0,且c是不等式组$\left\{\begin{array}{l}{\frac{x+12}{4}≤x+6}\\{\frac{2x+2}{3}>x-3}\end{array}\right.$的最大整数解,试求△ABC的三边长;
(2)在(1)的条件得到满足的△ABC中,若设AE=m,则当m满足什么条件时,BE分△ABC的周长的差不小于2?
分析 (1)根据a2+b2-16a-12b+100=0,且c是不等式组$\left\{\begin{array}{l}{\frac{x+12}{4}≤x+6}\\{\frac{2x+2}{3}>x-3}\end{array}\right.$的最大整数解,可以分别求得a、b、c的值,然后根据勾股定理的逆定理可以判断△ABC的形状;
(2)由题意可以得到关于m的不等式,从而可以解答本题.
解答 解:(1)∵a2+b2-16a-12b+100=0,
∴(a-8)2+(b-6)2=0,
∴a-8=0,b-6=0,
得a=8,b=6,
解$\left\{\begin{array}{l}{\frac{x+12}{4}≤x+6}\\{\frac{2x+2}{3}>x-3}\end{array}\right.$
得,-4≤x<11,
∵c是不等式组$\left\{\begin{array}{l}{\frac{x+12}{4}≤x+6}\\{\frac{2x+2}{3}>x-3}\end{array}\right.$的最大整数解,
∴c=10,
∵a=8,b=8,c=10,62+82=102,
∴△ABC是直角三角形;
(2)由题意可得,
|(AB+AE)-(BC+CE)|≥2,
即|(10+m)-(8+6-m)|≥2,
解得,m≥3或m≤1,
即当m≥3或m≤1时,BE分△ABC的周长的差不小于2.
点评 本题考查一元一次不等式组的应用,勾股定理的逆定理,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
19.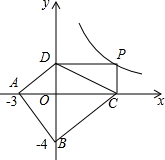 如图,已知A(-3,0),B(0,-4),P为反比例函数y=$\frac{12}{x}$(x>0)图象上的动点,PC⊥x轴于C,PD⊥y轴于D,则四边形ABCD面积的最小值为( )
如图,已知A(-3,0),B(0,-4),P为反比例函数y=$\frac{12}{x}$(x>0)图象上的动点,PC⊥x轴于C,PD⊥y轴于D,则四边形ABCD面积的最小值为( )
 如图,已知A(-3,0),B(0,-4),P为反比例函数y=$\frac{12}{x}$(x>0)图象上的动点,PC⊥x轴于C,PD⊥y轴于D,则四边形ABCD面积的最小值为( )
如图,已知A(-3,0),B(0,-4),P为反比例函数y=$\frac{12}{x}$(x>0)图象上的动点,PC⊥x轴于C,PD⊥y轴于D,则四边形ABCD面积的最小值为( )| A. | 12 | B. | 13 | C. | 24 | D. | 26 |
20.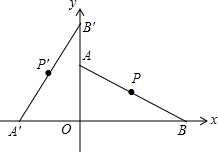 如图,在平面直角坐标系中,A(0,$2\sqrt{3}$),B(6,0),点P为线段AB的中点,将线段AB绕点O逆时针旋转90°后点P的对应点P′的坐标是( )
如图,在平面直角坐标系中,A(0,$2\sqrt{3}$),B(6,0),点P为线段AB的中点,将线段AB绕点O逆时针旋转90°后点P的对应点P′的坐标是( )
 如图,在平面直角坐标系中,A(0,$2\sqrt{3}$),B(6,0),点P为线段AB的中点,将线段AB绕点O逆时针旋转90°后点P的对应点P′的坐标是( )
如图,在平面直角坐标系中,A(0,$2\sqrt{3}$),B(6,0),点P为线段AB的中点,将线段AB绕点O逆时针旋转90°后点P的对应点P′的坐标是( )| A. | (-3,$\sqrt{3}$) | B. | ($-\sqrt{3}$,3) | C. | ($\sqrt{3}$,-3) | D. | (-1,$\sqrt{3}$) |
17.已知反比例函数y=-$\frac{3}{x}$,下列结论不正确的是( )
| A. | 图象必经过点(-1,3) | B. | 两个分支分布在第二、四象限 | ||
| C. | 若x>1,则-3<y<0 | D. | y随x的增大而增大 |
5.在-$\frac{5}{3}$,-$\sqrt{2}$,-$\sqrt{3}$,-$\frac{π}{2}$四个数中,最大的数是( )
| A. | -$\frac{5}{3}$ | B. | -$\sqrt{2}$ | C. | -$\sqrt{3}$ | D. | -$\frac{π}{2}$ |
12.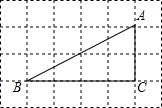 如图,△ABC的顶点都是正方形网格中的格点,则cosA等于( )
如图,△ABC的顶点都是正方形网格中的格点,则cosA等于( )
 如图,△ABC的顶点都是正方形网格中的格点,则cosA等于( )
如图,△ABC的顶点都是正方形网格中的格点,则cosA等于( )| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\sqrt{5}$ | D. | $\frac{2}{3}$ |
 如图,正方形ABCD中,AB=2,点E为BC边上的一个动点,连接AE,作∠EAF=45°,交CD边于点F,连接EF.若设BE=x,则△CEF的周长为4.
如图,正方形ABCD中,AB=2,点E为BC边上的一个动点,连接AE,作∠EAF=45°,交CD边于点F,连接EF.若设BE=x,则△CEF的周长为4.