题目内容
12.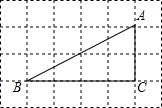 如图,△ABC的顶点都是正方形网格中的格点,则cosA等于( )
如图,△ABC的顶点都是正方形网格中的格点,则cosA等于( )| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\sqrt{5}$ | D. | $\frac{2}{3}$ |
分析 利用勾股定理先求得斜边长,进而求得∠A的邻边与斜边之比即可.
解答 解:由格点可得∠A所在的直角三角形的两条直角边为2,4,
∴斜边为$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$.
∴cos∠A=$\frac{2}{2\sqrt{5}}$=$\frac{\sqrt{5}}{5}$.
故选B.
点评 考查了锐角三角函数的定义,难点是利用勾股定理求得∠A所在的直角三角形的斜边长,关键是理解余弦等于邻边比斜边.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
2.下列运算中,结果等于a5的是( )
| A. | a2+a3 | B. | a10÷a2 | C. | a3•a2 | D. | (a2)3 |
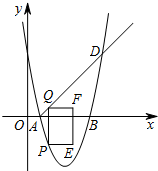 如图,在平面直角坐标系中,抛物线y=ax2+bx+5与x轴交于A(1,0)、B(5,0)两点,点D是抛物线上横坐标为6的点.点P在这条抛物线上,且不与A、D两点重合,过点P作y轴的平行线与射线AD交于点Q,过点Q作QF垂直于y轴,点F在点Q的右侧,且QF=2,以QF、QP为邻边作矩形QPEF.设矩形QPEF的周长为d,点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=ax2+bx+5与x轴交于A(1,0)、B(5,0)两点,点D是抛物线上横坐标为6的点.点P在这条抛物线上,且不与A、D两点重合,过点P作y轴的平行线与射线AD交于点Q,过点Q作QF垂直于y轴,点F在点Q的右侧,且QF=2,以QF、QP为邻边作矩形QPEF.设矩形QPEF的周长为d,点P的横坐标为m.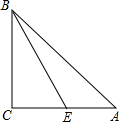 已知:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,点E是AC边上的一个动点(点E与点A、C不重合).
已知:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,点E是AC边上的一个动点(点E与点A、C不重合).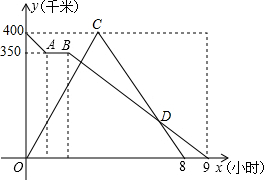 甲、乙两地相距的路程是400千米,快、慢两车同时从两地出发,慢车从乙地驶向甲地,中途因故停车1小时后,继续按原路原速驶向甲地;快车从甲地驶向乙地,在到达乙地后,立即按原路原速返回到甲地,在两车行驶的过程中,两车距甲地的路程y(千米)与两车行驶时间x(小时)之间的函数图象如图所示.请结合图象解答下列间题:
甲、乙两地相距的路程是400千米,快、慢两车同时从两地出发,慢车从乙地驶向甲地,中途因故停车1小时后,继续按原路原速驶向甲地;快车从甲地驶向乙地,在到达乙地后,立即按原路原速返回到甲地,在两车行驶的过程中,两车距甲地的路程y(千米)与两车行驶时间x(小时)之间的函数图象如图所示.请结合图象解答下列间题: