题目内容
10. 如图,正方形ABCD中,AB=2,点E为BC边上的一个动点,连接AE,作∠EAF=45°,交CD边于点F,连接EF.若设BE=x,则△CEF的周长为4.
如图,正方形ABCD中,AB=2,点E为BC边上的一个动点,连接AE,作∠EAF=45°,交CD边于点F,连接EF.若设BE=x,则△CEF的周长为4.
分析 先根据正方形的性质得AB=AD,∠BAD=∠B=90°,把△ADF绕点A顺时针旋转90°可得到△ABG,接着利用“SAS”证明△EAG≌△EAF,得到EG=EF=BE+DF,然后利用三角形周长的定义得到△CEF的周长=CE+CF+BE+DF=CB+CD,由此即可解决问题.
解答 解 :∵四边形ABCD为正方形,
:∵四边形ABCD为正方形,
∴AB=AD,∠BAD=∠B=90°,
∴把△ADF绕点A顺时针旋转90°可得到△ABG,如图,
∴AG=AF,BG=DF,∠GAF=90°,∠ABG=∠B=90°,
∴点G在CB的延长线上,
∵∠EAF=45°,
∴∠EAG=∠GAF-∠EAF=45°,
∴∠EAG=∠EAF,
在△EAG和△EAF中,
$\left\{\begin{array}{l}{AE=AE}\\{∠EAG=∠EAF}\\{AG=AF}\end{array}\right.$,
∴△EAG≌△EAF(SAS),
∴EG=EF,
而EG=BE+BG=BE+DF,
∴EF=BE+DF,
∴△CEF的周长=CE+CF+BE+DF=CB+CD=2+2=4.
故答案为4.
点评 本题考查了全等三角形的判定与性质、正方形的性质等知识,解题的关键是利用旋转添加辅助线构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
18.若反比例函数y=$\frac{k}{x}$的图象位于第二、四象限,则k的取值可能是( )
| A. | -1 | B. | 2 | C. | 3 | D. | 4 |
15.对于一次函数y=-x+2,下列结论错误的是( )
| A. | y随着x的增大而减小 | |
| B. | 函数图象不经过第三象限 | |
| C. | 函数图象向下平移2个单位长度得到y=-x的图象 | |
| D. | 函数图象与x轴的交点是(0,2) |
2.下列运算中,结果等于a5的是( )
| A. | a2+a3 | B. | a10÷a2 | C. | a3•a2 | D. | (a2)3 |
19.下列运算中,计算结果正确的是( )
| A. | x3+x3=x6 | B. | (-4m2n)2=16m4n2 | C. | (-a)3•a2=-a6 | D. | 3a-2=$\frac{1}{3{a}^{2}}$ |
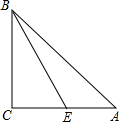 已知:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,点E是AC边上的一个动点(点E与点A、C不重合).
已知:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,点E是AC边上的一个动点(点E与点A、C不重合).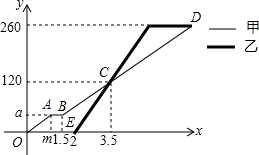 甲、乙两台机器各自加工相同数量的零件,工作时工作效率不变,甲机器先开始工作,中途停机检修了0.5小时.如图是甲、乙两台机器在整个工作过程中各自加工的零件个数y(个)与甲机器工作时间x(时)之间的函数图象.
甲、乙两台机器各自加工相同数量的零件,工作时工作效率不变,甲机器先开始工作,中途停机检修了0.5小时.如图是甲、乙两台机器在整个工作过程中各自加工的零件个数y(个)与甲机器工作时间x(时)之间的函数图象.