题目内容
9.直线y=kx-2k+4(k≠0)与抛物线y=-x2+4x-3有唯一公共点,求k的值.分析 根据图象有唯一公共点,可得判别式等于零,根据解方程,可得答案.
解答 解:由y=kx-2k+4(k≠0)与抛物线y=-x2+4x-3有唯一公共点,得
x2+(k-4)x+7-2k=0,
△=b2-4ac=(k-4)2-4(7-2k)=0
解得k=±2$\sqrt{3}$,
y=kx-2k+4(k≠0)与抛物线y=-x2+4x-3有唯一公共点,k的值是±2$\sqrt{3}$.
点评 本题考查了二次函数的性质,利用图象有唯一公共点得出判别式等于零是解题关键.

练习册系列答案
相关题目
18.若反比例函数y=$\frac{k}{x}$的图象位于第二、四象限,则k的取值可能是( )
| A. | -1 | B. | 2 | C. | 3 | D. | 4 |
19.下列运算中,计算结果正确的是( )
| A. | x3+x3=x6 | B. | (-4m2n)2=16m4n2 | C. | (-a)3•a2=-a6 | D. | 3a-2=$\frac{1}{3{a}^{2}}$ |

 已知:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,点E是AC边上的一个动点(点E与点A、C不重合).
已知:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,点E是AC边上的一个动点(点E与点A、C不重合).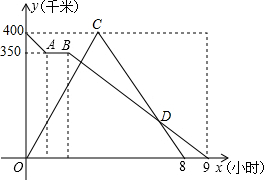 甲、乙两地相距的路程是400千米,快、慢两车同时从两地出发,慢车从乙地驶向甲地,中途因故停车1小时后,继续按原路原速驶向甲地;快车从甲地驶向乙地,在到达乙地后,立即按原路原速返回到甲地,在两车行驶的过程中,两车距甲地的路程y(千米)与两车行驶时间x(小时)之间的函数图象如图所示.请结合图象解答下列间题:
甲、乙两地相距的路程是400千米,快、慢两车同时从两地出发,慢车从乙地驶向甲地,中途因故停车1小时后,继续按原路原速驶向甲地;快车从甲地驶向乙地,在到达乙地后,立即按原路原速返回到甲地,在两车行驶的过程中,两车距甲地的路程y(千米)与两车行驶时间x(小时)之间的函数图象如图所示.请结合图象解答下列间题: