题目内容
4.已知,平面直角坐标系中的点A(a,1),t=ab-a2-b2(a,b是实数)(1)若关于x的反比例函数y=$\frac{{a}^{2}}{x}$过点A,求t的取值范围.
(2)若关于x的一次函数y=bx过点A,求t的取值范围.
(3)若关于x的二次函数y=x2+bx+b2过点A,求t的取值范围.
分析 (1)把点A的坐标代入反比例函数解析式求得a的值;然后利用二次函数的最值的求法得到t的取值范围.
(2)把点A的坐标代入一次函数解析式求得a=$\frac{1}{b}$;然后利用二次函数的最值的求法得到t的取值范围.
(3)把点A的坐标代入二次函数解析式求得以a2+b2=1-ab;然后利用非负数的性质得到t的取值范围.
解答 解:(1)把A(a,1)代入y=$\frac{{a}^{2}}{x}$得到:1=$\frac{{a}^{2}}{a}$,
解得a=1,
则t=ab-a2-b2=b-1-b2=-(b-$\frac{1}{2}$)2-$\frac{3}{4}$.
因为抛物线t=-(b-$\frac{1}{2}$)2-$\frac{3}{4}$的开口方向向下,且顶点坐标是($\frac{1}{2}$,-$\frac{3}{4}$),
所以t的取值范围为:t≤-$\frac{3}{4}$;
(2)把A(a,1)代入y=bx得到:1=ab,
所以a=$\frac{1}{b}$,
则t=ab-a2-b2=-(a2+b2)+1=-(b+$\frac{1}{b}$)2+3≤3,
故t的取值范围为:t≤3;
(3)把A(a,1)代入y=x2+bx+b2得到:1=a2+ab+b2,
所以ab=1-(a2+b2),
则t=ab-a2-b2=1-2(a2+b2)≤1,
故t的取值范围为:t≤1.
点评 本题考查了反比例函数、一次函数以及二次函数的性质.代入求值时,注意配方法的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
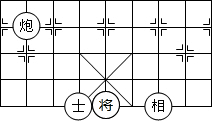 中国象棋在中国有着三千多年的历史,它难易适中,趣味性强,变化丰富细腻,棋盘棋子文字都体现了中国文化.如图,如果
中国象棋在中国有着三千多年的历史,它难易适中,趣味性强,变化丰富细腻,棋盘棋子文字都体现了中国文化.如图,如果 所在位置的坐标为(-1,-1),
所在位置的坐标为(-1,-1), 所在位置的坐标为(2,-1),那么,
所在位置的坐标为(2,-1),那么, 所在位置的坐标为(-3,2).
所在位置的坐标为(-3,2).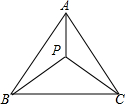 如图,等边△ABC中,AB=4,P是△ABC中的任意一点,连接PA、PB、PC,则PA+PB+PC的最小值为4$\sqrt{3}$.
如图,等边△ABC中,AB=4,P是△ABC中的任意一点,连接PA、PB、PC,则PA+PB+PC的最小值为4$\sqrt{3}$.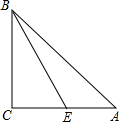 已知:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,点E是AC边上的一个动点(点E与点A、C不重合).
已知:如图,在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,点E是AC边上的一个动点(点E与点A、C不重合).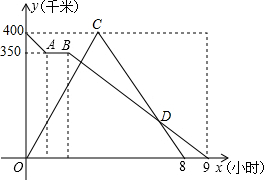 甲、乙两地相距的路程是400千米,快、慢两车同时从两地出发,慢车从乙地驶向甲地,中途因故停车1小时后,继续按原路原速驶向甲地;快车从甲地驶向乙地,在到达乙地后,立即按原路原速返回到甲地,在两车行驶的过程中,两车距甲地的路程y(千米)与两车行驶时间x(小时)之间的函数图象如图所示.请结合图象解答下列间题:
甲、乙两地相距的路程是400千米,快、慢两车同时从两地出发,慢车从乙地驶向甲地,中途因故停车1小时后,继续按原路原速驶向甲地;快车从甲地驶向乙地,在到达乙地后,立即按原路原速返回到甲地,在两车行驶的过程中,两车距甲地的路程y(千米)与两车行驶时间x(小时)之间的函数图象如图所示.请结合图象解答下列间题: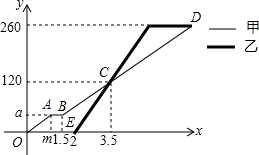 甲、乙两台机器各自加工相同数量的零件,工作时工作效率不变,甲机器先开始工作,中途停机检修了0.5小时.如图是甲、乙两台机器在整个工作过程中各自加工的零件个数y(个)与甲机器工作时间x(时)之间的函数图象.
甲、乙两台机器各自加工相同数量的零件,工作时工作效率不变,甲机器先开始工作,中途停机检修了0.5小时.如图是甲、乙两台机器在整个工作过程中各自加工的零件个数y(个)与甲机器工作时间x(时)之间的函数图象.