题目内容
13.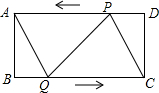 如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P、Q的速度的速度都是1cm/s,连结PQ,AQ,CP,设点P、Q运动的时间为t(s).
如图,在矩形ABCD中,AB=4cm,BC=8cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P、Q的速度的速度都是1cm/s,连结PQ,AQ,CP,设点P、Q运动的时间为t(s).(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.
分析 (1)当四边形ABQP是矩形时,BQ=AP,据此求得t的值;
(2)当四边形AQCP是菱形时,AQ=AC,列方程求得运动的时间t;
(3)菱形的四条边相等,则菱形的周长=4t,面积=矩形的面积-2个直角三角形的面积.
解答 解:(1)当四边形ABQP是矩形时,BQ=AP,即:t=8-t,
解得t=4.
答:当t=4时,四边形ABQP是矩形;
(2)设t秒后,四边形AQCP是菱形
当AQ=CQ,即$\sqrt{{4}^{2}+{t}^{2}}$=8-t时,四边形AQCP为菱形.
解得:t=3.
答:当t=3时,四边形AQCP是菱形;
(3)当t=3时,CQ=5,则周长为:4CQ=20cm,
面积为:4×8-2×$\frac{1}{2}$×3×4=20(cm2).
点评 本题考查了菱形、矩形的判定与性质.解决此题注意结合方程的思想解题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
14.不等式$-\frac{1}{2}≤\frac{1-0.6x}{-3}≤\frac{2}{3}$的整数解的个数为( )
| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
1.下列各实数中,无理数是( )
| A. | $\sqrt{4}$ | B. | 0 | C. | $\root{3}{9}$ | D. | ($\sqrt{2}$)0 |
3.如果a=(-99)0,b=(-0.1)-1,C=($-\frac{5}{3}$)-2,那么a、b、c的大小关系为( )
| A. | a>c>b | B. | c>a>b | C. | a>b>c | D. | c>b>a |
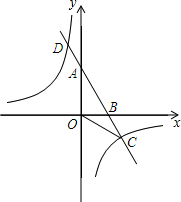 如图,已知A,B两点的坐标分别是A(0,2$\sqrt{3}$),B(2,0),直线AB与反比例函数y=$\frac{m}{x}$的图象交于点C和点D(-1,a).
如图,已知A,B两点的坐标分别是A(0,2$\sqrt{3}$),B(2,0),直线AB与反比例函数y=$\frac{m}{x}$的图象交于点C和点D(-1,a).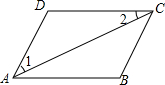 如图,AC平分∠DAB,∠1=∠2,请结合图形填空:
如图,AC平分∠DAB,∠1=∠2,请结合图形填空: 如图,x=60,y=50.
如图,x=60,y=50.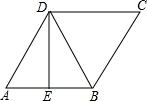 如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,求∠ABD的度数.
如图,在菱形ABCD中,E是AB的中点,且DE⊥AB,求∠ABD的度数.