题目内容
9.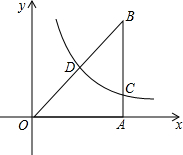 已知,Rt△OAB在直角坐标系内的位置如图所示,BA⊥OA,点B(4,4),反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过线段OB的中点D,且与直线AB交于点C.
已知,Rt△OAB在直角坐标系内的位置如图所示,BA⊥OA,点B(4,4),反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过线段OB的中点D,且与直线AB交于点C.(1)求直线OB的解析式;
(2)求反比例函数的解析式;
(3)联结OC,直接写出△OCB的面积.
分析 (1)根据函数图象和点B(4,4),可以求得直线OB的解析式;
(2)根据点B(4,4),反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过线段OB的中点D,可以求得点D的坐标,从而可以求得反比例函数的解析式;
(3)根据已知条件可以求得点A、C的坐标,从而可以求得△OCB的面积.
解答 解:(1)设直线OB的函数解析式为y=kx,
4=4k,解得k=1,
即直线OB的解析式是y=x;
(2)∵反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过线段OB的中点D,点B(4,4),
∴点D的坐标是(2,2),
∴$2=\frac{k}{2}$,
解得,k=4,
即反比例函数的解析式是$y=\frac{4}{x}$;
(3)连接OC,如右图所示,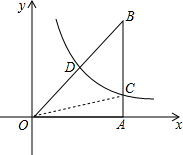
当x=4时,$y=\frac{4}{4}$=1,
∴点C的坐标是(4,1),
∵点A(4,0),AC=1,AB=4,
∴S△OCB=S△OAB-S△OAC=$\frac{4×4}{2}-\frac{4×1}{2}=6$,
即△OCB的面积是6.
点评 本题考查反比例函数与一次函数的交点问题,解题的关键是明确题意,利用数形结合的思想找出所求问题需要的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知平行四边形ABCD中,∠A=2∠B,则∠C=( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
11.使分式$\frac{x+3}{2x-8}$有意义的x值是( )
| A. | x=4 | B. | x=-3 | C. | x≠4 | D. | x=≠-3 |
1.下列各实数中,无理数是( )
| A. | $\sqrt{4}$ | B. | 0 | C. | $\root{3}{9}$ | D. | ($\sqrt{2}$)0 |
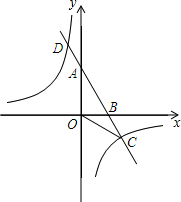 如图,已知A,B两点的坐标分别是A(0,2$\sqrt{3}$),B(2,0),直线AB与反比例函数y=$\frac{m}{x}$的图象交于点C和点D(-1,a).
如图,已知A,B两点的坐标分别是A(0,2$\sqrt{3}$),B(2,0),直线AB与反比例函数y=$\frac{m}{x}$的图象交于点C和点D(-1,a). 如图,在菱形ABCD中,点P在对角线BD上,CP的延长线交AD于点E,交BA的延长线于点F,求证:△APE∽△FPA.
如图,在菱形ABCD中,点P在对角线BD上,CP的延长线交AD于点E,交BA的延长线于点F,求证:△APE∽△FPA. 如图,x=60,y=50.
如图,x=60,y=50.