题目内容
4.若函数y=$\left\{\begin{array}{l}{{x}^{2}-2(x≤2)}\\{2x(x>2)}\end{array}\right.$,则当函数值y=8时,自变量x的值是( )| A. | ±$\sqrt{6}$ | B. | 4 | C. | ±$\sqrt{6}$或4 | D. | 4或-$\sqrt{6}$ |
分析 把y=8直接代入函数y=$\left\{\begin{array}{l}{{x}^{2}-2(x≤2)}\\{2x(x>2)}\end{array}\right.$,即可求出自变量的值.
解答 解:把y=8代入函数y=$\left\{\begin{array}{l}{{x}^{2}-2(x≤2)}\\{2x(x>2)}\end{array}\right.$,
先代入上边的方程得x=±$\sqrt{6}$,
∵x≤2,x=$\sqrt{6}$,不合题意舍去,故x=-$\sqrt{6}$;
再代入下边的方程x=4,∵x>2,故x=4,
综上,x的值为4或-$\sqrt{6}$.
故选D
点评 本题考查求函数值及二次函数的性质:(1)当已知函数解析式时,求函数值就是求代数式的值;(2)函数值是唯一的,而对应的自变量可以是多个.

练习册系列答案
相关题目
14. 如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( )
如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( )
 如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( )
如图,在△ABC中,∠C=90°,∠A=30°,∠ABC的平分线BD交AC于D,DE⊥AB于点C,若DE=3cm,则AC=( )| A. | 9cm | B. | 6cm | C. | 12cm | D. | 3cm |
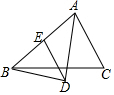 如图,△ABC中,AD平分∠BAC,BD⊥AD,DE∥AC,求证:DE=$\frac{1}{2}$AB.
如图,△ABC中,AD平分∠BAC,BD⊥AD,DE∥AC,求证:DE=$\frac{1}{2}$AB.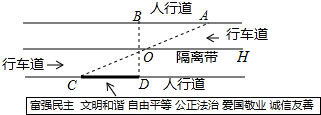 杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下,如图,AB∥OH∥CD,相邻两平行线间的距离相等.AC,BD相交于O,OD⊥CD垂足为D.已知AB=20米.根据上述信息,标语CD的长度为20m.
杨阳同学沿一段笔直的人行道行走,在由A步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下,如图,AB∥OH∥CD,相邻两平行线间的距离相等.AC,BD相交于O,OD⊥CD垂足为D.已知AB=20米.根据上述信息,标语CD的长度为20m. 如图,AA′,BB′,CC′相交于点O,且A′B′∥AB,B′C′∥BC,A′C′∥AC,OB=3OB′,判断△ABC的面积与△A′B′C′的面积有什么关系?
如图,AA′,BB′,CC′相交于点O,且A′B′∥AB,B′C′∥BC,A′C′∥AC,OB=3OB′,判断△ABC的面积与△A′B′C′的面积有什么关系? 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为$\frac{18}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB交于点D,则AD的长为$\frac{18}{5}$.