题目内容
19.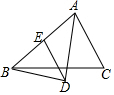 如图,△ABC中,AD平分∠BAC,BD⊥AD,DE∥AC,求证:DE=$\frac{1}{2}$AB.
如图,△ABC中,AD平分∠BAC,BD⊥AD,DE∥AC,求证:DE=$\frac{1}{2}$AB.
分析 根据角平分线的定义得到∠BAD=∠CAD,根据平行线的性质得到∠ADE=∠CAD,等量代换得到∠ADE=∠EAD,根据等腰三角形的判定得到AE=DE,由直角三角形的性质即刻得到结论.
解答 解:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠ADE=∠CAD,
∴∠ADE=∠EAD,
∴AE=DE,
∵AD⊥BD,
∴∠ADB=90°,
∴∠EAD+∠ABD=∠ADE+∠BDE=90°,
∴∠EBD=∠BDE,
∴BE=DE,
∴DE=$\frac{1}{2}$AB.
点评 本题考查了等腰三角形的判定和性质,角平分线的定义,平行线的性质,熟练掌握等腰三角形的判定和性质是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
2.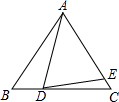 如图所示,在△ABC中,AB=AC,∠BAD=α,且AE=AD,则∠EDC=( )
如图所示,在△ABC中,AB=AC,∠BAD=α,且AE=AD,则∠EDC=( )
 如图所示,在△ABC中,AB=AC,∠BAD=α,且AE=AD,则∠EDC=( )
如图所示,在△ABC中,AB=AC,∠BAD=α,且AE=AD,则∠EDC=( )| A. | $\frac{1}{4}$α | B. | $\frac{1}{3}$α | C. | $\frac{1}{2}$α | D. | $\frac{2}{3}$α |
4.若函数y=$\left\{\begin{array}{l}{{x}^{2}-2(x≤2)}\\{2x(x>2)}\end{array}\right.$,则当函数值y=8时,自变量x的值是( )
| A. | ±$\sqrt{6}$ | B. | 4 | C. | ±$\sqrt{6}$或4 | D. | 4或-$\sqrt{6}$ |
9.方程x2-2x=0的解为( )
| A. | x=2 | B. | x=0 | C. | x1=0 或 x2=2 | D. | x1=0 或 x2=-2 |
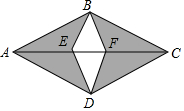 如图是某房间木地板的一个图案,其中AB=BC=CD=DA,BE=DE=DF=FB,图案由有花纹的全等三角形木块(阴影部分)和无花纹的全等三角形木块(中间部分)拼成,这个图案的面积是0.05m2.若房间的面积是23m2,问最少需要有花纹的三角形木块和无花纹的木块各多少块?
如图是某房间木地板的一个图案,其中AB=BC=CD=DA,BE=DE=DF=FB,图案由有花纹的全等三角形木块(阴影部分)和无花纹的全等三角形木块(中间部分)拼成,这个图案的面积是0.05m2.若房间的面积是23m2,问最少需要有花纹的三角形木块和无花纹的木块各多少块? 如图,A、B在直线l异侧,在直线l上取一点P,使PA+PB最小.
如图,A、B在直线l异侧,在直线l上取一点P,使PA+PB最小.