题目内容
10.2$\sqrt{x-2y+4}$=0,则代数式$\frac{x+y}{2}$•$\frac{x-y}{x-2y}$÷$\frac{{x}^{2}-{y}^{2}}{{x}^{2}-4xy+4{y}^{2}}$的值是-2.分析 先把分子分母因式分解,再把除法运算化为乘法运算,约分得到原式=$\frac{x-2y}{2}$,然后根据算术平方根的定义得到x-2y+4=0,则x-2y=-4,再利用整体代入的方法计算.
解答 解:原式=$\frac{x+y}{2}$•$\frac{x-y}{x-2y}$•$\frac{(x-2y)^{2}}{(x+y)(x-y)}$
=$\frac{x-2y}{2}$,
∵2$\sqrt{x-2y+4}$=0,
∴x-2y+4=0,即x-2y=-4,
∴原式=$\frac{-4}{2}$=-2.
故答案为-2.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
18.若|m-n-3|+(m+n+1)2=0,则m+2n的值为( )
| A. | -1 | B. | -3 | C. | 0 | D. | 3 |
19.已知k、b是一元二次方程(x+1)(x-1)=0的两个根,且k<b,则函数y=kx+b的图象不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,已知AB=10,P是线段AB上任意一点,在AB的同侧分别以AP和PB为边作等边△APC和等边△BPD,则CD长度的最小值为5.
如图,已知AB=10,P是线段AB上任意一点,在AB的同侧分别以AP和PB为边作等边△APC和等边△BPD,则CD长度的最小值为5.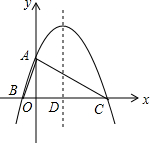 如图,已知二次函数y=ax2+bx+4的图象与y轴交于点A,与x轴交于B(-2,0)、C(8,0)两点,其对称轴与x轴交于点D,连接AC、AB.
如图,已知二次函数y=ax2+bx+4的图象与y轴交于点A,与x轴交于B(-2,0)、C(8,0)两点,其对称轴与x轴交于点D,连接AC、AB.