题目内容
解下列方程:
(1)3(x-5)2=2(5-x)
(2)2x2-8x+2=0.
(1)3(x-5)2=2(5-x)
(2)2x2-8x+2=0.
考点:解一元二次方程-因式分解法,解一元二次方程-配方法
专题:
分析:(1)先移项,再提公因式即可;
(2)先系数化为1,再配方即可.
(2)先系数化为1,再配方即可.
解答:解:(1)3(x-5)2=-2(x-5),
3(x-5)2+2(x-5)=0,
(x-5)[3(x-5)+2]=0,
x-5=0或3x-13=0,
解得x1=5,x2=
;
(2)x2-4x+1=0,
x2-4x=-1,
x2-4x+4=3,
(x-2)2=3,
x-2=±
,
x=±
+2,
x1=
+2,x2=-
+2.
3(x-5)2+2(x-5)=0,
(x-5)[3(x-5)+2]=0,
x-5=0或3x-13=0,
解得x1=5,x2=
| 13 |
| 3 |
(2)x2-4x+1=0,
x2-4x=-1,
x2-4x+4=3,
(x-2)2=3,
x-2=±
| 3 |
x=±
| 3 |
x1=
| 3 |
| 3 |
点评:本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
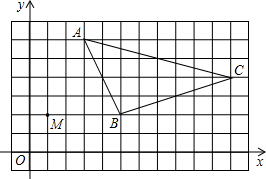 在如图所示网格图中,已知△ABC和点M(1,2)
在如图所示网格图中,已知△ABC和点M(1,2) 如图,在坡角为30°的斜坡上有两棵树,它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为
如图,在坡角为30°的斜坡上有两棵树,它们之间的水平距离AC为6m,则这两棵树之间的坡面AB的长为 已知有理数a,b,c在数轴上的位置如图所示,化简:|a+b|-|b-4|-|a-c|+|1-c|.
已知有理数a,b,c在数轴上的位置如图所示,化简:|a+b|-|b-4|-|a-c|+|1-c|.