Question

6．如图，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，AB=AE，BE的延长线分别交AD、AC的延长线于点F、G．
（1）求证：AF=FG．
（2）已知tanG=$\frac{1}{2}$，求sin∠CBG的值．

Answer 1

分析 （1）根据圆周角定理得出∠BAC=90°，进而得出∠ACB=∠ABE，∠G=∠CAD，即可得出答案；
（2）设CD=1，则AD=2，BE=AH=2AD=4，AC=$\sqrt{5}$，再得出△ABC∽△DAC，进而求出sin∠CBG的值．

解答 （1）证明：连接AB，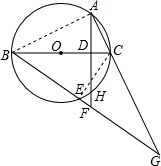
∵BC是⊙O的直径，
∴∠BAC=90°，
则∠G+∠ABE=90°，
∵AD⊥BC，
∴∠CAD+∠ACB=90°，
∵$\widehat{AB}$=$\widehat{AE}$，
∴∠ACB=∠ABE，
∴∠G=∠CAD，
∴AF=FG；

（2）解：连接CE，设AF与⊙O交于H，
∵AD⊥BC，
∴AD=DH，$\widehat{AB}$=$\widehat{BH}$，
∵$\widehat{AB}$=$\widehat{AE}$，
∴$\widehat{ABE}$=$\widehat{ABH}$，
∴BE=AH，
∵tan∠CAD=$\frac{CD}{AD}$=tan∠G=$\frac{1}{2}$，
设CD=1，则AD=2，BE=AH=2AD=4，AC=$\sqrt{5}$，
∵∠BAC=∠ADC=90°，∠ACD=∠BCA，
∴△ABC∽△DAC，
∴$\frac{AC}{CD}$=$\frac{BC}{AC}$，
∴BC=$\frac{AC•AC}{DC}$=5，
∵BC是直径，则∠BEC=90°，
∴EC=3，
∴sin∠CBG=$\frac{CE}{BC}$=$\frac{3}{5}$．

点评 此题主要考查了垂径定理以及相似三角形的判定与性质等知识，正确得出△ABC∽△DAC是解题关键．