题目内容
11.已知a(a-2)-(a2-2b)=-4.求$\frac{{a}^{2}+{b}^{2}}{-2-ab}$的值.分析 由a(a-2)-(a2-2b)=-4整理可得a-b=2,代入$\frac{{a}^{2}+{b}^{2}}{-2-ab}$=$\frac{(a-b)^{2}+2ab}{-(2+ab)}$整理后约分可得.
解答 解:由a(a-2)-(a2-2b)=-4得:a2-2a-a2+2b=-4,
整理,得:a-b=2,
∴$\frac{{a}^{2}+{b}^{2}}{-2-ab}$=$\frac{(a-b)^{2}+2ab}{-(2+ab)}$
=$\frac{4+2ab}{-(2+ab)}$
=$\frac{2(2+ab)}{-(2+ab)}$
=-2.
点评 本题主要考查完全平方公式,熟练掌握完全平方公式和将完全平方公式灵活变形是解题的关键,同时也考查了整体代入的思想.

练习册系列答案
相关题目
20. 某小学三年级到六年级的全体学生参加“礼仪”知识测试,试题共有10题,每题10分.从中随机抽取了部分学生的成绩进行统计,发现抽测的学生每人至少答对了6题,现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”.
某小学三年级到六年级的全体学生参加“礼仪”知识测试,试题共有10题,每题10分.从中随机抽取了部分学生的成绩进行统计,发现抽测的学生每人至少答对了6题,现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”.
成绩情况统计表
根据图表中提供的信息,回答下列问题:
(1)测试学生中,成绩为80分的学生人数有36名;众数是90分;中位数是90分;
(2)若该小学三年级到六年级共有1800名学生,则可估计出成绩为70分的学生人数约有270名.
 某小学三年级到六年级的全体学生参加“礼仪”知识测试,试题共有10题,每题10分.从中随机抽取了部分学生的成绩进行统计,发现抽测的学生每人至少答对了6题,现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”.
某小学三年级到六年级的全体学生参加“礼仪”知识测试,试题共有10题,每题10分.从中随机抽取了部分学生的成绩进行统计,发现抽测的学生每人至少答对了6题,现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”.成绩情况统计表
| 成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
| 人数 | 21 | 40 | 36 | 18 | 5 |
| 频率 | 0.175 | 0.333 | 0.3 | 0.15 | 0.04 |
(1)测试学生中,成绩为80分的学生人数有36名;众数是90分;中位数是90分;
(2)若该小学三年级到六年级共有1800名学生,则可估计出成绩为70分的学生人数约有270名.
20.下列运算中,正确的是( )
| A. | a2•a4=a8 | B. | (a2)3=a6 | C. | a+a3=a4 | D. | (a+b)(a-b)=a2+b2 |
1.如图①,在?ABCD中,∠B=120°,动点P从点B出发,沿BC、CD、DA运动至点A停止.设点P运动的路程为xcm,△PAB的面积为ycm2,y关于x的函数的图象如图②所示,则图②中H点的横坐标为( )
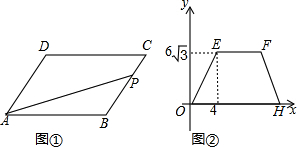

| A. | 11 | B. | 14 | C. | 8+$\frac{3}{2}\sqrt{3}$ | D. | 8+3$\sqrt{3}$ |
 如图,正方形ABCD的边长为4,延长CB至点M,使BM=2,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为$\frac{6\sqrt{10}}{5}$.
如图,正方形ABCD的边长为4,延长CB至点M,使BM=2,过点B作BN⊥AM,垂足为N,O是对角线AC,BD的交点,连接ON,则ON的长为$\frac{6\sqrt{10}}{5}$. 如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.
如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G. 如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,AB=AE,BE的延长线分别交AD、AC的延长线于点F、G.
如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,AB=AE,BE的延长线分别交AD、AC的延长线于点F、G.