题目内容
15．
在一个边长不超过8厘米的大正方形ABCD中，如图所示，放入3张面积都是20平方厘米的小正方形纸片BEFG、OPNC、IQKJ，已知3张小正方形纸片盖住的总面积为44平方厘米，那么大正方形ABCD和小正方形BEFG的边长之比为（ ）| A． | 5：3 | B． | 3：2 | C． | 10：7 | D． | 8：5 |
分析 将正方形IQKJ平移使左边与大正方形左边重合（红色），设右上角未被盖住部分的面积为x平方厘米，列出方程求出x，然后求出正方形边长即可．
解答 解：将正方形IQKJ平移使左边与大正方形左边重合（红色），三个正方形覆盖的总面积不变，
这时，大正方形被分成四个部分，蓝色正方形面积为20平方厘米，
红、黄两块显露的矩形面积相等，其面积和是44-20=24平方厘米，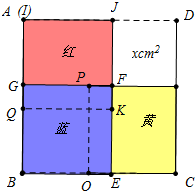
所以红黄两矩形面积均为12平方厘米，
设右上角未被盖住部分的面积为x平方厘米（如图）
则12：20=x：12
20x=12×12
20x=144
x=7.2
因此大正方形的面积为44+7.2=51.2（平方厘米），
所以大正方形ABCD边长为$\sqrt{51.2}$，正方形BEFG的边长为$\sqrt{20}$，
所以大正方形ABCD和小正方形BEFG的边长之比为$\sqrt{51.2÷20}$=$\sqrt{2.56}$=1.6=$\frac{8}{5}$．
故选D．
点评 本题考查正方形的性质、解题的关键是通过平移三个正方形覆盖的总面积不变，设未知数列出方程解决问题，学会把不规则图形变成规则图形解决，属于中考常考题型．
练习册系列答案
相关题目
10．
如图，已知△ABC，∠C=90°，∠A=30°，AC=$\sqrt{3}$，动点D在边AC上，以BD为边作等边△BDE（点E、A在BD的同侧），在点D从点A移动至点C的过程中，点E移动的路线为（ ）
如图，已知△ABC，∠C=90°，∠A=30°，AC=$\sqrt{3}$，动点D在边AC上，以BD为边作等边△BDE（点E、A在BD的同侧），在点D从点A移动至点C的过程中，点E移动的路线为（ ）| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | $\frac{π}{3}$ | D． | $\frac{2π}{3}$ |
20．
某小学三年级到六年级的全体学生参加“礼仪”知识测试，试题共有10题，每题10分．从中随机抽取了部分学生的成绩进行统计，发现抽测的学生每人至少答对了6题，现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”．
成绩情况统计表
根据图表中提供的信息，回答下列问题：
（1）测试学生中，成绩为80分的学生人数有36名；众数是90分；中位数是90分；
（2）若该小学三年级到六年级共有1800名学生，则可估计出成绩为70分的学生人数约有270名．
某小学三年级到六年级的全体学生参加“礼仪”知识测试，试题共有10题，每题10分．从中随机抽取了部分学生的成绩进行统计，发现抽测的学生每人至少答对了6题，现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”．成绩情况统计表
| 成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
| 人数 | 21 | 40 | 36 | 18 | 5 |
| 频率 | 0.175 | 0.333 | 0.3 | 0.15 | 0.04 |
（1）测试学生中，成绩为80分的学生人数有36名；众数是90分；中位数是90分；
（2）若该小学三年级到六年级共有1800名学生，则可估计出成绩为70分的学生人数约有270名．
7．
据国家教育部、卫生部最新调查表明：我国小学生近视率超过25%，初中生近视率达到70%，每年以8%的速度增长，居世界第一位．某市为调查中学生视力情况，从全市九年级学生中抽取了部分学生，统计了每个人连续三年视力检查的结果，并将所得数据处理后，制成统计表和扇形统计图如下：
被抽取学生视力在4.9以下的人数变化情况统计表
解答下列问题：
（1）扇形统计图中x=10；
（2）该市共抽取了九年级学生2000名；
（3）若该市今年共有九年级学生约8.5万名，请你估计该市九年级学生视力不良（4.9以下）的学生大约有多少名？
据国家教育部、卫生部最新调查表明：我国小学生近视率超过25%，初中生近视率达到70%，每年以8%的速度增长，居世界第一位．某市为调查中学生视力情况，从全市九年级学生中抽取了部分学生，统计了每个人连续三年视力检查的结果，并将所得数据处理后，制成统计表和扇形统计图如下：被抽取学生视力在4.9以下的人数变化情况统计表
| 年份 | 2014 | 2015 | 2016 |
| 人数 | 300 | 500 | 800 |
（1）扇形统计图中x=10；
（2）该市共抽取了九年级学生2000名；
（3）若该市今年共有九年级学生约8.5万名，请你估计该市九年级学生视力不良（4.9以下）的学生大约有多少名？
如图，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，AB=AE，BE的延长线分别交AD、AC的延长线于点F、G．
7．
某移动公司近日推出了如下两种月收费方式．
已知k，l满足$\left\{\begin{array}{l}{2l-7k=1}\\{5k-l=10}\end{array}\right.$设每月的通话时间为x分钟，A、B两种收费方式的收费金额分别为yA元、yB元．
（I）求k，1的值．
（2）如图是yB与x之间的函数关系图象，请根据图象填空：m=10，n=50．
（3）写出yA与x之间的函数关系式．
（4）选择哪种收费方式较合算？为什么？
某移动公司近日推出了如下两种月收费方式．| 收费方式 | 月租费/元 | 赠送通话时间/分钟 | 超时费/（元/分钟） |
| A | k | l | 0.2 |
| B | m | n | 0.1 |
（I）求k，1的值．
（2）如图是yB与x之间的函数关系图象，请根据图象填空：m=10，n=50．
（3）写出yA与x之间的函数关系式．
（4）选择哪种收费方式较合算？为什么？