题目内容
7.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点P(-2,6),则k的值是( )| A. | -3 | B. | 3 | C. | 12 | D. | -12 |
分析 根据反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点P(-2,6),从而可以求得k的值.
解答 解:∵反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点P(-2,6),
∴$6=\frac{k}{-2}$,得k=-12,
故选D.
点评 本题考查反比例函数图象上点的坐标特征,解答本题的关键是明确题意,利用反比例函数的性质解答.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
17. 如图,△ABC与△DEF关于直线MN轴对称,则下列结论中错误的是( )
如图,△ABC与△DEF关于直线MN轴对称,则下列结论中错误的是( )
 如图,△ABC与△DEF关于直线MN轴对称,则下列结论中错误的是( )
如图,△ABC与△DEF关于直线MN轴对称,则下列结论中错误的是( )| A. | AB∥DF | B. | ∠B=∠E | ||
| C. | AB=DE | D. | AD的连线被MN垂直平分 |
18.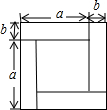 如图,将完全相同的四个长方形纸片拼成一个大的正方形,用两种不同的方法表示这个大正方形的面积,则可以得出一个等式为( )
如图,将完全相同的四个长方形纸片拼成一个大的正方形,用两种不同的方法表示这个大正方形的面积,则可以得出一个等式为( )
 如图,将完全相同的四个长方形纸片拼成一个大的正方形,用两种不同的方法表示这个大正方形的面积,则可以得出一个等式为( )
如图,将完全相同的四个长方形纸片拼成一个大的正方形,用两种不同的方法表示这个大正方形的面积,则可以得出一个等式为( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | C. | a2-b2=(a+b)(a-b) | D. | (a+b)2=(a-b)2+4ab |
2.用配方法解一元二次方程:2y2+2y-1=0,配方后得( )
| A. | (y-1)2=$\frac{3}{2}$ | B. | (y+1)2=$\frac{3}{2}$ | C. | (y+$\frac{1}{2}$)2=$\frac{3}{4}$ | D. | (y-$\frac{1}{2}$)2=$\frac{3}{4}$ |
12. 某学校拟建一间矩形活动室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,建成后的活动室面积为75m2,求矩形活动室的长和宽,若设矩形宽为x,根据题意可列方程为( )
某学校拟建一间矩形活动室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,建成后的活动室面积为75m2,求矩形活动室的长和宽,若设矩形宽为x,根据题意可列方程为( )
 某学校拟建一间矩形活动室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,建成后的活动室面积为75m2,求矩形活动室的长和宽,若设矩形宽为x,根据题意可列方程为( )
某学校拟建一间矩形活动室,一面靠墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1m宽的门,已知计划中的材料可建墙体(不包括门)总长为27m,建成后的活动室面积为75m2,求矩形活动室的长和宽,若设矩形宽为x,根据题意可列方程为( )| A. | x(27-3x)=75 | B. | x(3x-27)=75 | C. | x(30-3x)=75 | D. | x(3x-30)=75 |
19. 如图,函数y=2x和y=ax+4的图象相交于点A($\frac{3}{2}$,3),则不等式2x<ac+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A($\frac{3}{2}$,3),则不等式2x<ac+4的解集为( )
 如图,函数y=2x和y=ax+4的图象相交于点A($\frac{3}{2}$,3),则不等式2x<ac+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A($\frac{3}{2}$,3),则不等式2x<ac+4的解集为( )| A. | x<$\frac{3}{2}$ | B. | x<3 | C. | x>$\frac{3}{2}$ | D. | x>3 |
16.已知a=$\sqrt{2}$+1,b=$\frac{1}{\sqrt{2}-1}$,则a,b的大小关系是( )
| A. | a>b | B. | a=b | C. | a<b | D. | 无法确定 |
17.-2的绝对值是( )
| A. | $\frac{1}{2}$ | B. | -2 | C. | 2 | D. | -$\frac{1}{2}$ |
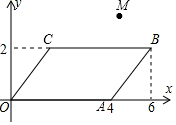 如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,且A(4,0)、B(6,2)、M(4,3).在平面内有一条过点M的直线将平行四边形OABC的面积分成相等的两部分,请写出该直线的函数表达式y=2x-5.
如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,且A(4,0)、B(6,2)、M(4,3).在平面内有一条过点M的直线将平行四边形OABC的面积分成相等的两部分,请写出该直线的函数表达式y=2x-5.