题目内容
18.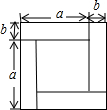 如图,将完全相同的四个长方形纸片拼成一个大的正方形,用两种不同的方法表示这个大正方形的面积,则可以得出一个等式为( )
如图,将完全相同的四个长方形纸片拼成一个大的正方形,用两种不同的方法表示这个大正方形的面积,则可以得出一个等式为( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | C. | a2-b2=(a+b)(a-b) | D. | (a+b)2=(a-b)2+4ab |
分析 根据题意表示出图形的边长进而得出其面积.
解答 解:由图形可得:大正方形的边长为:a+b,则其面积为:(a+b)2,
小正方形的边长为:(a-b),则其面积为:(a-b)2,长方形面积为:ab,
故(a+b)2=(a-b)2+4ab.
故选:D.
点评 此题主要考查了完全平方公式的几何背景,正确表示出各边长是解题关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
9.如果分式$\frac{{{m^2}-4}}{m-2}$的值为零,那么m的值是( )
| A. | m≠2 | B. | m=±2 | C. | m=-2 | D. | m=2 |
13.下列运算错误的是( )
| A. | a+2a=3a | B. | (a2)3=a6 | C. | a2•a3=a5 | D. | a6÷a3=a2 |
3.数据:3,4,3,5,6中,众数和中位数分别为( )
| A. | 3,3 | B. | 2,3 | C. | 3,4 | D. | 3,3.5 |
7.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过点P(-2,6),则k的值是( )
| A. | -3 | B. | 3 | C. | 12 | D. | -12 |
8.下面调查方式中正确的是( )
| A. | 了解某品牌灯泡的使用寿命用全面调查的方式 | |
| B. | 学校招聘教师,对应聘人员面试用抽样调查的方式 | |
| C. | 旅客上飞机前的安检用全面调查的方式 | |
| D. | 纠正某书稿中的错别字用抽样调查的方式 |
 如图,已知∠A=∠AGE,∠D=∠DGC.
如图,已知∠A=∠AGE,∠D=∠DGC.
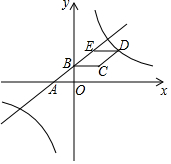 如图,在平面直角坐标系中,菱形BCDE的一边BC平行于x轴,点D在第一象限,直线y=$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,并经过点E,且点B是AE的中点,店D在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.
如图,在平面直角坐标系中,菱形BCDE的一边BC平行于x轴,点D在第一象限,直线y=$\frac{3}{4}$x+3与x轴交于点A,与y轴交于点B,并经过点E,且点B是AE的中点,店D在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.