题目内容
5．某个密码锁的密码由三个数字组成，每个数字都是0-9这十个数字中的一个，只有当三个数字与所设定的密码及顺序完全相同时，才能将锁打开．如果仅忘记了锁设密码的最后那个数字，那么一次就能打开该密码的概率是（ ）| A． | $\frac{1}{10}$ | B． | $\frac{1}{9}$ | C． | $\frac{1}{3}$ | D． | $\frac{1}{2}$ |
分析 最后一个数字可能是0～9中任一个，总共有十种情况，其中开锁只有一种情况，利用概率公式进行计算即可．
解答 解：∵共有10个数字，
∴一共有10种等可能的选择，
∵一次能打开密码的只有1种情况，
∴一次能打开该密码的概率为$\frac{1}{10}$．
故选A．
点评 此题考查了概率公式的应用．注意概率=所求情况数与总情况数之比．
练习册系列答案
相关题目
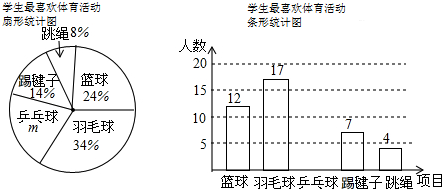
15．为了解七年级学生上学期参加社会实践活动的情况，随机抽查A市七年级部分学生参加社会实践活动天数，并根据抽查结果制作了如下不完整的频数分布表和条形统计图．
A市七年级部分学生参加社会实践活动天数的频数分布表
A市七年级部分学生参加社会实践活动天数的条形统计图
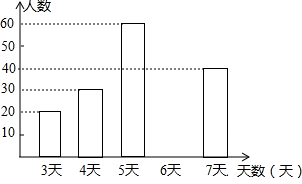
根据以上信息，解答下列问题；
（1）求出频数分布表中a的值，并补全条形统计图．
（2）A市有七年级学生20000人，请你估计该市七年级学生参加社会实践活动不少于5天的人数．
A市七年级部分学生参加社会实践活动天数的频数分布表
| 天数 | 频数 | 频率 |
| 3 | 20 | 0.10 |
| 4 | 30 | 0.15 |
| 5 | 60 | 0.30 |
| 6 | a | 0.25 |
| 7 | 40 | 0.20 |
根据以上信息，解答下列问题；
（1）求出频数分布表中a的值，并补全条形统计图．
（2）A市有七年级学生20000人，请你估计该市七年级学生参加社会实践活动不少于5天的人数．
16．
如图，AB∥CD，DE⊥CE，∠1=34°，则∠DCE的度数为（ ）
如图，AB∥CD，DE⊥CE，∠1=34°，则∠DCE的度数为（ ）| A． | 34° | B． | 54° | C． | 66° | D． | 56° |
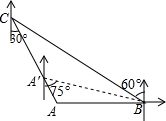如图，“中国海监50”正在南海海域A处巡逻，岛礁B上的中国海军发现点A在点B的正西方向上，岛礁C上的中国海军发现点A在点C的南偏东30°方向上，已知点C在点B的北偏西60°方向上，且B、C两地相距120海里．
如图，矩形ABCD的对角线AC，BD相交于点O，若AB=AO，求∠ABD的度数．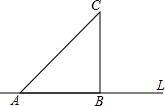
如图，等腰直角三角形ABC的一直角边AB在直线L上，将该三角形绕着顶点B顺时针方向旋转，至边BC落在直线L上，再绕顶点C顺时针旋转至边CA落在直线L上，若AB=1，则顶点A的运动轨迹与直线L围成的图形的面积是π+$\frac{1}{2}$．
如图，在平面直角坐标系中，有一个直角△ABC，且A（-1，3），B（-3，-1），C（-3，3），已知△A1A1C是由△ABC旋转得到的．