题目内容
13.定义:对角线互相垂直的凸四边形叫做“垂直四边形”.(1)理解:如图1,已知四边形ABCD是“垂直四边形”,对角线AC,BD交于点O,AC=8,BD=7,求四边形ABCD的面积.
(2)探究:小明对“垂直四边形”ABCD(如图1)进行了深入探究,发现其一组对边的平方和等于另一组对边的平方和.即AB2+CD2=AD2+BC2.你认为他的发现正确吗?试说明理由.
(3)应用:
①如图2,在△ABC中,∠ACB=90°,AC=6,BC=8,动点P从点A出发沿AB方向以每秒5个单位的速度向点B匀速运动,同时动点Q从点C出发沿CA方向以每秒6个单位的速度向点A匀速运动,运动时间为t秒(0<t<1),连结CP,BQ,PQ.当四边形BCQP是“垂直四边形”时,求t的值.
②如图3,在△ABC中,∠ACB=90°,AB=3AC,分别以AB,AC为边向外作正方形ABDE和正方形ACFG,连结EG.请直接写出线段EG与BC之间的数量关系.

分析 (1)由于对角线互相垂直,所以四边形ABCD的面积可化为$\frac{1}{2}AO•BD$+$\frac{1}{2}CO•BD$的和;
(2)由于对角线互相垂直,由勾股定理分别表示出AB2、CD2、AD2、BC2;
(3)①过点P作PD⊥AC于点D,构造△PAD∽△BAC后,利用BP2+CQ2=PQ2+BC2列出关于t的方程;
②连接BE、CG、BG、CE,证明四边形BCGE是垂直四边形,然后利用其性质“一组对边的平方和等于另一组对边的平方和”,即可得出EG与BC的数量关系.
解答 解:(1)∵四边形ABCD是“垂直四边形”,
∴AC⊥BD,
∴△ABD的面积为:$\frac{1}{2}AO•BD$,
△CBD的面积为:$\frac{1}{2}CO•BD$,
∴四边形ABCD的面积:$\frac{1}{2}AO•BD$+$\frac{1}{2}CO•BD$
=$\frac{1}{2}$BD(AO+CO)
=$\frac{1}{2}$AC•BD
=$\frac{1}{2}$×8×7
=28;
(2)∵四边形ABCD是“垂直四边形”,
∴AC⊥BD.
由勾股定理可知:
AB2+CD2=(AO2+BO2)+(DO2+CO2),
AD2+BC2=(AO2+DO2)+(BO2+CO2),
∴AB2+CD2=AD2+BC2; (3)①如图2,过点P作PD⊥AC于点D,
(3)①如图2,过点P作PD⊥AC于点D,
由题意知:AP=5t,CQ=6t,
∵∠ACB=90°,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10
∵PD∥BC.
∴△PAD∽△BAC,
∴$\frac{AD}{AC}$=$\frac{PD}{BC}$=$\frac{AP}{AB}$,
∴$\frac{AD}{6}$=$\frac{PD}{8}$=$\frac{5t}{10}$,
∴AD=3t,PD=4t,
∴DQ=AC-AD-CQ=6-9t,
∵四边形BCQP是“垂直四边形”.
∴BP2+CQ2=PQ2+BC2,
∴(10-5t)2+(6t)2=(4t)2+(6-9t)2+82,
∴解得t=$\frac{2}{9}$或t=0(舍去),
∴当四边形BCQP是“垂直四边形”时,t的值为$\frac{2}{9}$;
②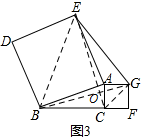 如图3,连接CG、BG、BE、CE,
如图3,连接CG、BG、BE、CE,
CE与BG交于点O
由题意知:EA=BA,AC=AG
∠EAB=∠CAG=90°
∴∠EAB+∠BAC=∠CAG+∠BAC
∴∠EAC=∠BAG
在△EAC与△BAG中
$\left\{\begin{array}{l}{EA=BA}\\{∠EAC=∠BAG}\\{AC=AG}\end{array}\right.$,
∴△EAC≌△BAG(SAS)
∴∠CEA=∠GBA
∴∠EAB=∠BOE=90°
∴四边形BCGE是“垂直四边形”
∴BC2+EG2=BE2+CG2,
∵AB=3AC,
∴EG2=$\frac{3}{2}$BC2.
点评 本题考查新定义型问题,解题的关键是对新定义的理解,涉及到勾股定理,全等三角形的性质与判定,相似三角形的性质与判定等知识内容,题目较新颖和综合,需要学生将新旧知识联系起来.

 某学校计划开设A、B、C、D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如下所示的两个不完整统计图表.
某学校计划开设A、B、C、D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如下所示的两个不完整统计图表.校本课程选修意向统计表
| 选修课程 | 所占百分比 |
| A | a% |
| B | 25% |
| C | b% |
| D | 20% |
(1)参与调查的学生有100名;
(2)在统计表中,a=40,b=15,请你补全条形统计图;
(3)若该校共有2000名学生,请你估算该校有多少名学生选修A课程?
| A. | x>2 | B. | x≥2 | C. | x≤2 | D. | x≠2 |
 如图,在平面直角坐标系中,有一个直角△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1A1C是由△ABC旋转得到的.
如图,在平面直角坐标系中,有一个直角△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1A1C是由△ABC旋转得到的.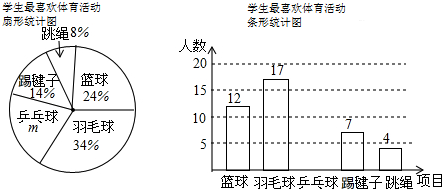
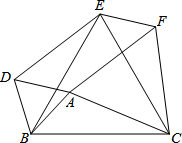 如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.
如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.