题目内容
9.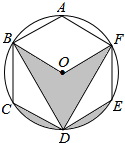 如图所示,正六边形ABCDEF内接于⊙O,若⊙O的半径为8,则阴影部分的面积等于$\frac{64}{3}$π.
如图所示,正六边形ABCDEF内接于⊙O,若⊙O的半径为8,则阴影部分的面积等于$\frac{64}{3}$π.
分析 首先连接OC,OE,分别交BD,DF于点M,N,易证得S△OBM=S△DCM,同理:S△OFN=S△DEN,则可得S阴影=S扇形OCE.
解答 解:连接OC,OE,分别交BD,DF于点M,N,如图所示: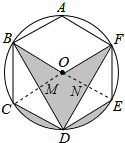
∵正六边形ABCDEF内接于⊙O,
∴∠BOC=60°,∠BCD=∠COE=120°,
∵OB=OC,
∴△OBC是等边三角形,
∴∠OBC=∠OCB=60°,
∴∠OCD=∠OCB,
∵BC=CD,
∴∠CBD=∠CDM=30°,BM=DM,
∴∠OBM=30°,S△DCM=S△BCM,
∴∠OBM=∠CBD,
∴OM=CM,
∴S△OBM=S△BCM,
∴S△OBM=S△DCM,
同理:S△OFN=S△DEN,
∴S阴影=S扇形OCE=$\frac{120π×{8}^{2}}{360}$=$\frac{64}{3}$π.
故答案为:$\frac{64}{3}$π.
点评 此题考查了正多边形与圆的知识以及扇形的面积公式.注意证得S阴影=S扇形OCE是关键.

练习册系列答案
相关题目
20.以下说法合理的是( )
| A. | 小明在10次抛图钉的试验中发现3次钉朝上,由此他说钉尖朝上的概率是30% | |
| B. | 抛掷一枚普通的正六面体骰子,出现6的概率是$\frac{1}{6}$的意思是每6次就有1次掷得6 | |
| C. | 某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖 | |
| D. | 在一次课堂进行的抛掷硬币试验中,某同学估计硬币落地后,正面朝上的概率为$\frac{1}{2}$ |
 如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数.
如图,矩形ABCD的对角线AC,BD相交于点O,若AB=AO,求∠ABD的度数.
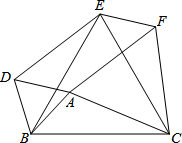 如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.
如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.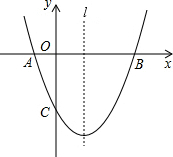 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,-3)三点,直线l是抛物线的对称轴.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,-3)三点,直线l是抛物线的对称轴.