题目内容
已知实数a,b满足ab=1,M=
+
,N=
+
.
(1)试着取两组a,b的值,判断M与N的大小,并作出猜想.
(2)请用所学的数学知识验证你的猜想.
| a |
| a+1 |
| b |
| b+1 |
| 1 |
| a+1 |
| 1 |
| b+1 |
(1)试着取两组a,b的值,判断M与N的大小,并作出猜想.
(2)请用所学的数学知识验证你的猜想.
考点:分式的加减法
专题:计算题
分析:(1)取a与b两对值,代入M与N中计算,比较大小即可;
(2)利用作差法证明即可.
(2)利用作差法证明即可.
解答:解:(1)当a=2,b=
时,M=
+
=
+
=1,N=
+
=1;
当a=3,b=
时,M=
+
=1,N=
+
=1,
猜想M=N;
(2)M-N=
+
-
-
=
+
=
=
=
=0,
则M=N.
| 1 |
| 2 |
| 2 |
| 2+1 |
| ||
|
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
当a=3,b=
| 1 |
| 3 |
| 3 |
| 4 |
| ||
|
| 1 |
| 4 |
| 1 | ||
|
猜想M=N;
(2)M-N=
| a |
| a+1 |
| b |
| b+1 |
| 1 |
| a+1 |
| 1 |
| b+1 |
| a-1 |
| a+1 |
| b-1 |
| b+1 |
| ab+a-b-1+ab-a+b-1 |
| ab+a+b+1 |
| 2ab-2 |
| ab+a+b+1 |
| 2-2 |
| 2+a+b |
则M=N.
点评:此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
若多项式x2-2kxy-y2+xy-8化简后不含x、y的乘积项,则k的值为( )
| A、0 | ||
B、
| ||
C、-
| ||
D、
|
已知a-b=4,c+d=3,则(b+c)-(a-d)的值为( )
| A、-1 | B、1 | C、-5 | D、15 |
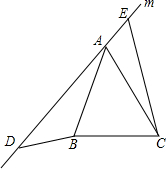 如图,在等腰三角形ABC中,已知AB=AC,∠BAC=α°,在过点A的直线m上取两点D,E,使得∠ADB=α°,∠AEC=α°.
如图,在等腰三角形ABC中,已知AB=AC,∠BAC=α°,在过点A的直线m上取两点D,E,使得∠ADB=α°,∠AEC=α°. 如图,直线MN∥PQ,直线GH交MN.PQ于点C.A,CD、AB分别平分∠GCN、∠QAN.试说明:直线CD⊥AB.
如图,直线MN∥PQ,直线GH交MN.PQ于点C.A,CD、AB分别平分∠GCN、∠QAN.试说明:直线CD⊥AB.