Question

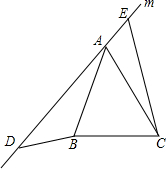如图，在等腰三角形ABC中，已知AB=AC，∠BAC=α°，在过点A的直线m上取两点D，E，使得∠ADB=α°，∠AEC=α°．
求证：△ADB≌△CEA．

Answer 1

考点：全等三角形的判定

专题：证明题

分析：欲证明△ADB≌△CEA，只需推知∠ABD=∠EAC．

解答：证明：∵∠BDA=∠BAC=α，
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α，
∴∠CAE=∠ABD，
在△ADB和△CEA中，

∠ABD=∠CAE ∠BDA=∠CEA AB=AC

，
∴△ADB≌△CEA（AAS）．

点评：本题考查了全等三角形的判定与性质：判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”；得出∠CAE=∠ABD是解题关键．