题目内容
因式分解: 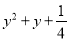 =______
=______
 【解析】根据完全平方公式进行因式分解为: .
故答案为:
.
【解析】根据完全平方公式进行因式分解为: .
故答案为:
.
练习册系列答案
相关题目
已知x=3是关于x的不等式3x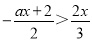 的解,求a的取值范围.
的解,求a的取值范围.
 a<4
【解析】试题分析:先根据不等式的解的定义,将x=3代入不等式3x,得到.
9,解此不等式,即可求出a的取值范围.
试题解析:∵x=3是关于x的不等式3x的解,
∴3×3.
整理 得3a<12,
解得a<4.
故a的取值范围是a<4.
a<4
【解析】试题分析:先根据不等式的解的定义,将x=3代入不等式3x,得到.
9,解此不等式,即可求出a的取值范围.
试题解析:∵x=3是关于x的不等式3x的解,
∴3×3.
整理 得3a<12,
解得a<4.
故a的取值范围是a<4. 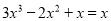 (______)
(______)
 【解析】根据提公因式法分解因式,可得=x().
故答案为: .
【解析】根据提公因式法分解因式,可得=x().
故答案为: . 下列从左到右的变形哪个是分解因式( )
A. 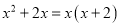 B.
B. 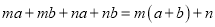
C. 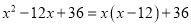 D.
D. 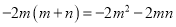
 A
【解析】根据因式分解的定义,可知因式分解是把一个多项式化为几个因式积的形式,可知A是因式分解.
故选:A.
A
【解析】根据因式分解的定义,可知因式分解是把一个多项式化为几个因式积的形式,可知A是因式分解.
故选:A. 如果x2+2(m-3)x+25能用公式法分解因式,那么m的值是多少?
 m=8或-2.
【解析】试题分析:利用完全平方公式的结构特征判断即可确定出m的值,注意包括两种情况.
试题解析:∵x2+2(m-3)x+25能用公式法分解因式,
∴2(m-3)=±10,
解得:m=8或-2.
m=8或-2.
【解析】试题分析:利用完全平方公式的结构特征判断即可确定出m的值,注意包括两种情况.
试题解析:∵x2+2(m-3)x+25能用公式法分解因式,
∴2(m-3)=±10,
解得:m=8或-2. 分解因式: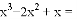 ______________.
______________.
 .
【解析】试题分析:==.故答案为:.
.
【解析】试题分析:==.故答案为:. 下列各式从左到右的变形中,是用公式法分解因式的是( )
A. 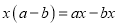 B.
B. 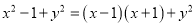
C. 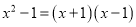 D.
D. 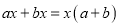
 C
【解析】根据平方差公式: ,完全平方公式: ,可知C选项的分解因式的方法是平方差公式,D选项是利用提公因式法分解因式,A、B不是分解因式.
故选:C.
C
【解析】根据平方差公式: ,完全平方公式: ,可知C选项的分解因式的方法是平方差公式,D选项是利用提公因式法分解因式,A、B不是分解因式.
故选:C. 如图,△ABC≌△CDA,且AD=CB,下列结论错误的是( )
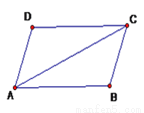
A. ∠B=∠D B. ∠CAB=∠ACD C. BC=CD D. AC=CA
 C
【解析】∵△ABC≌△CDA,
∴∠CAB=∠ACD,CA=AC,∠D=∠B,故A. B.D正确,不符合题意,
BC不一定等于CD,C错误,符合题意,
故选:C.
C
【解析】∵△ABC≌△CDA,
∴∠CAB=∠ACD,CA=AC,∠D=∠B,故A. B.D正确,不符合题意,
BC不一定等于CD,C错误,符合题意,
故选:C. 下列变形中,不正确的是( )
A. 由x-5>0可得x>5
B. 由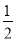 x>0可得x>0
x>0可得x>0
C. 由-3x>-9可得x>3
D. 由-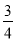 x>1可得x<-
x>1可得x<-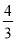
 C
【解析】A、在不等式两边同加上5,不等号不变,故正确;B、在不等式的两边同时乘以2,不等号不变,故正确;C、在不等式的两边同时除以-3,不等号方向改变,故错误;D、在不等式的两边同时乘以一个负数,不等号方向改变,故正确,
故先C.
C
【解析】A、在不等式两边同加上5,不等号不变,故正确;B、在不等式的两边同时乘以2,不等号不变,故正确;C、在不等式的两边同时除以-3,不等号方向改变,故错误;D、在不等式的两边同时乘以一个负数,不等号方向改变,故正确,
故先C. 
